题目内容
3．
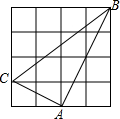如图，在4×4的正方形网格图中有△ABC，则sin∠ABC=（ ）| A． | $\frac{\sqrt{5}}{5}$ | B． | $\frac{2\sqrt{5}}{5}$ | C． | $\frac{1}{2}$ | D． | $\frac{3}{4}$ |
分析 先根据勾股定理的逆定理判断出△△ABC的形状，再由锐角三角函数的定义即可得出结论．
解答 解：∵AC2=12+22=5，AB2=42+22=20，BC2=32+42=25，
∴AC2+AB2=BC2，
∴△ABC是直角三角形，且∠BAC=90°，
∴sin∠ABC=$\frac{AC}{BC}$=$\frac{\sqrt{5}}{5}$．
故选A．
点评 本题考查的是勾股定理，先根据题意判断出△ABC的形状是解答此题的关键．
练习册系列答案
相关题目
14．
如图所示，一艘船从A点出发，沿东北方向航行至点B，再从B点出发沿南偏东15°方向航行至C点，则∠ABC的余角是（ ）
如图所示，一艘船从A点出发，沿东北方向航行至点B，再从B点出发沿南偏东15°方向航行至C点，则∠ABC的余角是（ ）| A． | 15° | B． | 30° | C． | 45° | D． | 75° |
11．某制药厂两年前生成1吨某种药品的成本是100万元，随着生产技术的进步，现在生产1吨这种药品的成本为81万元，设这种药品成本的年平均下降率为x，根据题意所列方程为（ ）
| A． | 100（1+x）2=81 | B． | 100（1-x）2=81 | C． | 81（1+x）2=100 | D． | 81（1-x）2=100 |
8．在0，-2，1，$\frac{1}{2}$这四个数中，最小的数是（ ）
| A． | 0 | B． | 1 | C． | -2 | D． | $\frac{1}{2}$ |
15．实数$\sqrt{41}$的小数部分是（ ）
| A． | 6-$\sqrt{41}$ | B． | $\sqrt{41}$-6 | C． | 7-$\sqrt{41}$ | D． | $\sqrt{41}$-7 |
