题目内容

15．实数$\sqrt{41}$的小数部分是（　　）
A．6-$\sqrt{41}$B．$\sqrt{41}$-6C．7-$\sqrt{41}$D．$\sqrt{41}$-7

分析 先估算出$\sqrt{41}$的取值范围，进而可得出结论．

解答 解：∵36＜41＜49，
∴6＜$\sqrt{41}$＜7，
∴$\sqrt{41}$的小数部分是$\sqrt{41}$-6，
故选B．

点评 本题考查的是估算无理数的大小，熟知估算无理数大小要用逼近法是解答此题的关键．

练习册系列答案
相关题目
5．点M（m+1，m+3）在y轴上，则M点的坐标为（　　）
A．（0，-4）B．（4，0）C．（-2，0）D．（0，2）
6．下列计算结果为正数的是（　　）
A．（-2）-2B．-（-2）0C．-|-2|D．（-2）3
3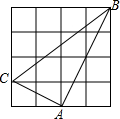．如图，在4×4的正方形网格图中有△ABC，则sin∠ABC=（　　）
A．$\frac{\sqrt{5}}{5}$B．$\frac{2\sqrt{5}}{5}$C．$\frac{1}{2}$D．$\frac{3}{4}$
10．若直线y=x+2与双曲线y=$\frac{m-3}{x}$在第二象限有两个交点，则m的取值范围是（　　）
A．m＞2B．m＜3C．2＜m＜3D．m＞3或m＜2
20．函数y=$\frac{5}{x}$与y=x+1的图象的交点坐标为（a，b），则a2+b2的值为（　　）
A．1B．11C．25D．无法求解
7．二元一次方程组$\left\{\begin{array}{l}{x-2y=5}\\{5x+4y=-3}\end{array}\right.$的解是（　　）
A．$\left\{\begin{array}{l}{x=-1}\\{y=-3}\end{array}\right.$B．$\left\{\begin{array}{l}{x=-\frac{7}{5}}\\{y=1}\end{array}\right.$C．$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$D．$\left\{\begin{array}{l}{x=2}\\{y=-\frac{3}{2}}\end{array}\right.$
4．如图，抛物线L：y=-$\frac{1}{2}$（x-t）（x-t+4）（常数t＞0）与x轴从左到右的交点为B，A，过线段OA的中点M作MP⊥x轴，交双曲线y=$\frac{k}{x}$（k＞0，x＞0）于点P，且OA•MP=12，
（1）求k值；
（2）当t=1时，求AB的长，并求直线MP与L对称轴之间的距离；
（3）把L在直线MP左侧部分的图象（含与直线MP的交点）记为G，用t表示图象G最高点的坐标；
（4）设L与双曲线有个交点的横坐标为x0，且满足4≤x0≤6，通过L位置随t变化的过程，直接写出t的取值范围．
5．解分式方程$\frac{1}{x-1}+1=0$，正确的结果是（　　）
A．x=0B．x=1C．x=2D．无解

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网