题目内容
10.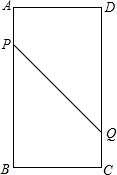 如图,在矩形ABCD中,AB=16cm,BC=6cm,点P从点A出发沿AB以3cm/s的速度向点B移动,一直到达点B为止;同时,点Q从点C出发沿CD以2cm/s的速度向点D移动.设运动的时间为t.
如图,在矩形ABCD中,AB=16cm,BC=6cm,点P从点A出发沿AB以3cm/s的速度向点B移动,一直到达点B为止;同时,点Q从点C出发沿CD以2cm/s的速度向点D移动.设运动的时间为t.(1)当t=$\frac{8}{5}$或$\frac{24}{5}$时,P、Q两点之间的距离是10cm?
(2)连PD,经过多长时间PD=PQ?
分析 (1)过点Q作QE⊥AB于点E,则四边形BCQE为矩形,找出线段AP、CQ、PE的长度,根据勾股定理结合PQ=10即可得出关于t的一元二次方程,解之即可得出结论;
(2)在Rt△APD中利用勾股定理找出PD的长度,结合PD=PQ即可得出关于t的一元二次方程,解之即可得出结论.
解答 解:(1)过点Q作QE⊥AB于点E,则四边形BCQE为矩形,如图所示.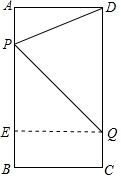
当运动时间为t秒时(0<t<$\frac{16}{3}$),AP=3t,CQ=2t,
∴PE=AB-AP-BE=AB-AP-CQ=16-5t.
在Rt△PEQ中,PE=16-5t,EQ=BC=6,
∴PQ2=PE2+EQ2=(16-5t)2+62=102,
解得:t1=$\frac{8}{5}$或t2=$\frac{24}{5}$.
故答案为:$\frac{8}{5}$或$\frac{24}{5}$.
(2)在Rt△APD中,AP=3t,AD=BC=6,
∴PD=$\sqrt{A{D}^{2}+A{P}^{2}}$=$\sqrt{(3t)^{2}+{6}^{2}}$.
∵PD=PQ,PQ=$\sqrt{(16-5t)^{2}+{6}^{2}}$,
∴$\sqrt{(3t)^{2}+{6}^{2}}$=$\sqrt{(16-5t)^{2}+{6}^{2}}$,即(3t)2=(16-5t)2,
解得:t1=2或t2=8(舍去).
答:经过2秒PD=PQ.
点评 本题考查了一元二次方程的应用、列代数式以及勾股定理,解题的关键是:(1)根据勾股定理结合PQ的长度列出关于t的一元二次方程;(2)根据勾股定理结合PD=PQ列出关于t的一元二次方程.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
7.为保护学生视力,课桌椅的高度都是按一定的关系配套设计的,研究表明:假设课桌的高度为ycm,椅子的高度为xcm,则y应是x 的一次函数,下表列出两套符合条件的课桌椅的高度:
(1)请确定y与x的函数关系式;
(2)现有一把高39cm的椅子和一张高为72.8的课桌,它们是否配套?为什么?
| 第一套 | 第二套 | |
| 椅子高度xcm | 40 | 37 |
| 桌子高度ycm | 75 | 70 |
(2)现有一把高39cm的椅子和一张高为72.8的课桌,它们是否配套?为什么?
19.单项式$\frac{1}{2}$x2y3的系数和次数分别是( )
| A. | 1,2 | B. | 2,3 | C. | $\frac{1}{2}$,5 | D. | $\frac{1}{2}$,2 |
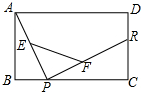 如图,矩形ABCD中,AD=13,DC=10,P是BC上的一点,R、E、F分别是DC、AP、RP的中点,当点P在BC上由B向C移动时,那么EF的长度$\frac{\sqrt{194}}{2}$.
如图,矩形ABCD中,AD=13,DC=10,P是BC上的一点,R、E、F分别是DC、AP、RP的中点,当点P在BC上由B向C移动时,那么EF的长度$\frac{\sqrt{194}}{2}$.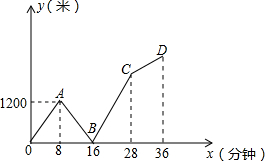 小明的爸爸和小明旱晨同时从家出发,以各自的速度匀速步行上班和上学,爸爸前往位于家正东方的公司,小明前往位于家正西方的学校,爸爸到达公司后发现小明的数学作业在自己的公文包里,于是立即跑步去小明,终于在途中追上了小明把作业给了他,然后再以先前的速度步行再回公司(途中给作业的时间忽略不计).结果爸爸回到公司的时间比小明到达学校的时间多用了8分钟.如图是两人之间的距离y(米)与他们从家出发的时间x(分钟)的函数关系图,则小明家与学校相距1800米.
小明的爸爸和小明旱晨同时从家出发,以各自的速度匀速步行上班和上学,爸爸前往位于家正东方的公司,小明前往位于家正西方的学校,爸爸到达公司后发现小明的数学作业在自己的公文包里,于是立即跑步去小明,终于在途中追上了小明把作业给了他,然后再以先前的速度步行再回公司(途中给作业的时间忽略不计).结果爸爸回到公司的时间比小明到达学校的时间多用了8分钟.如图是两人之间的距离y(米)与他们从家出发的时间x(分钟)的函数关系图,则小明家与学校相距1800米. 如图,∠C=45°,D在CA的延长线上,∠DAB的平分线交CB的延长线于点E,若∠EAB=75°,则∠ABC的度数为105°.
如图,∠C=45°,D在CA的延长线上,∠DAB的平分线交CB的延长线于点E,若∠EAB=75°,则∠ABC的度数为105°. 如图,在△ABC中,∠ACB=90°,E是AB的中点,AD∥EC,CD∥AB,试判断四边形ADCE的形状,并证明你的结论.
如图,在△ABC中,∠ACB=90°,E是AB的中点,AD∥EC,CD∥AB,试判断四边形ADCE的形状,并证明你的结论. 如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,连接EB,GD.且∠DAB=∠EAG
如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,连接EB,GD.且∠DAB=∠EAG