题目内容
2.若|x+1|+|x-1|的最小值记为n,|-x-1|-|x-1|的最大值记为m,则-nm=-4.分析 首先找到驻点,确定x的取值范围,分类讨论确定n和m的值,再计算-nm的值.
解答 解:因为|x+1|≥0,|x-1|≥0
当|x+1|=0时,x=-1;当|x-1|=0时,x=1.
当x=1或-1时,n=|x+1|+|x-1|=2.
因为当x≤-1时,|-x-1|-|x-1|=-x-1-(1-x)=-2;
当-1<x<1时,|-x-1|-|x-1|=x+1-(1-x)=2x,-2<2x<2;
当x≥1时,|-x-1|-|x-1|=x+1-(x-1)=2.
所以m=|-x-1|-|x-1|=2
所以-nm=-22=-4.
故答案为:-4.
点评 本题考查了绝对值的化简.运用分类讨论是解决本题的关键.

练习册系列答案
相关题目
7.比较$\sqrt{5}$,$\root{3}{7}$,2的大小,正确的是( )
| A. | $2<\sqrt{5}<\root{3}{7}$ | B. | $2<\root{3}{7}<\sqrt{5}$ | C. | $\root{3}{7}<2<\sqrt{5}$ | D. | $\sqrt{5}<\root{3}{7}<2$ |
14.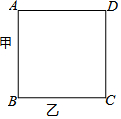 如图,某人沿着边长为90米的正方形,按A→C→D→B→A…方向运动,甲从A以64米/分的速度,乙从C以90米/分的速度行走,当乙第一次追上甲时在正方形的( )
如图,某人沿着边长为90米的正方形,按A→C→D→B→A…方向运动,甲从A以64米/分的速度,乙从C以90米/分的速度行走,当乙第一次追上甲时在正方形的( )
 如图,某人沿着边长为90米的正方形,按A→C→D→B→A…方向运动,甲从A以64米/分的速度,乙从C以90米/分的速度行走,当乙第一次追上甲时在正方形的( )
如图,某人沿着边长为90米的正方形,按A→C→D→B→A…方向运动,甲从A以64米/分的速度,乙从C以90米/分的速度行走,当乙第一次追上甲时在正方形的( )| A. | AB边上 | B. | CA边上 | C. | DC边上 | D. | BD边上 |
11.下列各式中,是方程的是( )
| A. | 7x-4=3x | B. | 4x-6 | C. | 4+3=7 | D. | 2x<5 |
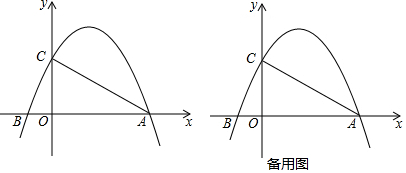
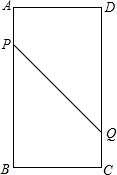 如图,在矩形ABCD中,AB=16cm,BC=6cm,点P从点A出发沿AB以3cm/s的速度向点B移动,一直到达点B为止;同时,点Q从点C出发沿CD以2cm/s的速度向点D移动.设运动的时间为t.
如图,在矩形ABCD中,AB=16cm,BC=6cm,点P从点A出发沿AB以3cm/s的速度向点B移动,一直到达点B为止;同时,点Q从点C出发沿CD以2cm/s的速度向点D移动.设运动的时间为t.