题目内容
20. 如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,连接EB,GD.且∠DAB=∠EAG
如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,连接EB,GD.且∠DAB=∠EAG(1)求证:EB=GD;
(2)若∠DAB=60°,AB=2,AG=$\sqrt{3}$,求GD的长.
分析 (1)只要证明△AEB≌△AGD即可解决问题.
(2)连接BD交AC于点P,则BP⊥AC,利用勾股定理求出线段EB即可解决问题.
解答 (1)证明:∵菱形AEFG∽菱形ABCD,
∴∠EAG=∠BAD,
∴∠EAG+∠GAB=∠BAD+∠GAB,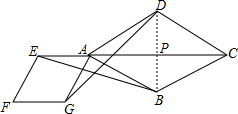
∴∠EAB=∠GAD,
∵AE=AG,AB=AD,
∴△AEB≌△AGD,
∴EB=GD;
(2)解:连接BD交AC于点P,则BP⊥AC,
∵∠DAB=60°,
∴∠PAB=30°,
∴BP=$\frac{1}{2}$AB=1,
AP=$\sqrt{A{B}^{2}-P{B}^{2}}$=$\sqrt{3}$,AE=AG=$\sqrt{3}$,
∴EP=2 $\sqrt{3}$,
∴EB=$\sqrt{E{P}^{2}+B{P}^{2}}$=$\sqrt{(2\sqrt{3})^{2}+{1}^{2}}$=$\sqrt{13}$,
∴GD=$\sqrt{13}$.
点评 本题考查菱形的性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是正确寻找全等三角形,学会用转化的思想思考问题,求线段DG转化为求线段EB,属于中考常考题型.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
11.下列各式中,是方程的是( )
| A. | 7x-4=3x | B. | 4x-6 | C. | 4+3=7 | D. | 2x<5 |
8.已知不等式x-1>0,此不等式的解在数轴上表示为( )
| A. |  | B. |  | C. |  | D. |  |
5.下列代数式中,是单项式的是( )
| A. | x+$\frac{1}{2}$ | B. | 5m-2m | C. | a | D. | $\frac{1}{a}$ |
12.在$\frac{π}{2}$,0,$-\sqrt{49}$,0.23,$\frac{22}{7}$,$\sqrt{3}$,0.3030030003,$1-\sqrt{2}$中,无理数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
9.$\sqrt{16}$的平方根与$-\root{3}{-8}$的算术平方根的和是( )
| A. | 6 | B. | 2 | C. | $±2+\sqrt{2}$ | D. | 4或0 |
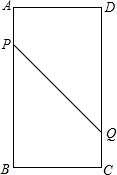 如图,在矩形ABCD中,AB=16cm,BC=6cm,点P从点A出发沿AB以3cm/s的速度向点B移动,一直到达点B为止;同时,点Q从点C出发沿CD以2cm/s的速度向点D移动.设运动的时间为t.
如图,在矩形ABCD中,AB=16cm,BC=6cm,点P从点A出发沿AB以3cm/s的速度向点B移动,一直到达点B为止;同时,点Q从点C出发沿CD以2cm/s的速度向点D移动.设运动的时间为t.