题目内容
2.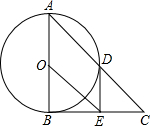 如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心,OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.
如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心,OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.(1)判断DE与⊙O的位置关系,并说明理由;
(2)若cos∠BAD=$\frac{3}{5}$,BE=$\frac{14}{3}$,求OE的长.
分析 (1)连结OD、BD,如图,根据圆周角定理得∠ADB=90°,再根据直角三角形斜边上的中线性质得ED=EB,则∠2=∠3,加上∠1=∠4,所以∠ODE=90°,然后根据切线得判断定理即可得到DE与⊙O相切;
(2)先证明OE为△BAC的中位线得到OE∥AC,则∠BAD=∠BOE,则在Rt△OBE中,利用余弦的定义得cos∠BOE=$\frac{OB}{OE}$=$\frac{3}{5}$,设OB=3x,则OE=5x,再利用勾股定理得到BE=4x,即4x=$\frac{14}{3}$,解得x=$\frac{7}{6}$,于是利用OE=5x求解.
解答 解:(1)DE与⊙O相切.理由如下:
连结OD、BD,如图,
∵AB为直径,
∴∠ADB=90°,
在Rt△BDC中,
∵E是BC的中点,
∴ED=EB,
∴∠2=∠3,
而OB=OD,
∴∠1=∠4,
∴∠3+∠4=∠1+∠2=90°,
即∠ODE=90°,
∴OD⊥DE,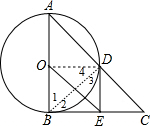
∴DE与⊙O相切;
(2)∵OA=OB,BE=CE,
∴OE为△BAC的中位线,
∴OE∥AC,
∴∠BAD=∠BOE,
∴cos∠BAD=cos∠BOE=$\frac{3}{5}$,
在Rt△OBE中,cos∠BOE=$\frac{OB}{OE}$=$\frac{3}{5}$,
设OB=3x,则OE=5x,
∴BE=$\sqrt{O{E}^{2}-O{B}^{2}}$=4x,
∴4x=$\frac{14}{3}$,解得x=$\frac{7}{6}$,
∴OE=5x=$\frac{35}{6}$.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了余弦的定义.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
14.我国海洋面积约为300万平方千米,近似于我国陆地面积的三分之一.将300万平方千米用科学记数法表示为( )
| A. | 3×102平方千米 | B. | 0.3×107平方千米 | C. | 3×106平方千米 | D. | 300×104平方千米 |
11.下列运算正确的是( )
| A. | a2•a3=a6 | B. | (a2)3=a5 | C. | (a2b3)2=a4b6 | D. | a3÷a4=a |
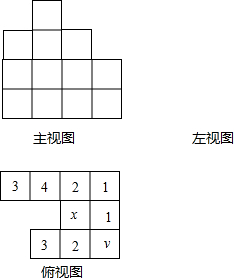 如图是几个小立方体搭成的几何体的俯视图,小正方形中的数字表示该位置上的小立方体的个数.
如图是几个小立方体搭成的几何体的俯视图,小正方形中的数字表示该位置上的小立方体的个数.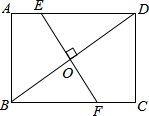 如图,在矩形ABCD中,AB=3cm,AD=4cm,过对角线BD的中点O作BD的垂线EF,分别交AD,BC于点E,F,求AE的长.
如图,在矩形ABCD中,AB=3cm,AD=4cm,过对角线BD的中点O作BD的垂线EF,分别交AD,BC于点E,F,求AE的长.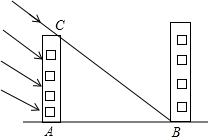 冬至是一年时间中太阳相对地球北半球位置最低的一天,只要这一天采到阳光,一年四季均能受到阳光的照射,此时竖立一根1米长的竹竿,其影长为1.5米,某单位计划建30米高的南北两栋办公楼,如图所示,问两楼相距多少米时,后楼的采光刚好一年四季都不受影响?
冬至是一年时间中太阳相对地球北半球位置最低的一天,只要这一天采到阳光,一年四季均能受到阳光的照射,此时竖立一根1米长的竹竿,其影长为1.5米,某单位计划建30米高的南北两栋办公楼,如图所示,问两楼相距多少米时,后楼的采光刚好一年四季都不受影响? 在某个奔跑活动中,有一个边长为10m正方形路线图,两名选手甲,乙同时从起点A沿着箭头方向绕路线图奔跑,两人第一次相遇在BC的中点O处,当两名选手第一次在点A处相遇时,选手乙已经跑了200m.
在某个奔跑活动中,有一个边长为10m正方形路线图,两名选手甲,乙同时从起点A沿着箭头方向绕路线图奔跑,两人第一次相遇在BC的中点O处,当两名选手第一次在点A处相遇时,选手乙已经跑了200m. 如图,是一个圆柱和一个长方体组成的几何体,圆柱的下底面紧贴在长方体的上底面上,那么这个几何体的主视图是( )
如图,是一个圆柱和一个长方体组成的几何体,圆柱的下底面紧贴在长方体的上底面上,那么这个几何体的主视图是( )


