题目内容
12.计算下列各题:(1)$\sqrt{32}-\sqrt{8}+2\sqrt{\frac{1}{2}}$;
(2)($\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})+(\sqrt{3}-1)^{2}$($\sqrt{5}-\sqrt{3}$)+($\sqrt{3}-1)^{2}$2.
分析 (1)先进行二次根式的化简,然后合并;
(2)先进行二次根式的乘法运算,然后合并.
解答 解:(1)原式=4$\sqrt{2}$-2$\sqrt{2}$+$\sqrt{2}$
=3$\sqrt{2}$;
(2)原式=2+4-2$\sqrt{3}$
=6-2$\sqrt{3}$.
点评 本题考查了二次根式的混合运算,解答本题的关键是掌握二次根式的乘法法则和二次根式的化简.

练习册系列答案
相关题目
4.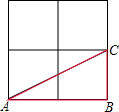 如图所示,△ABC是在2×2的正方形网格中以格点为顶点的三角形,那么图中与△ABC成轴对称且也以格点为顶点的三角形共有( )
如图所示,△ABC是在2×2的正方形网格中以格点为顶点的三角形,那么图中与△ABC成轴对称且也以格点为顶点的三角形共有( )
 如图所示,△ABC是在2×2的正方形网格中以格点为顶点的三角形,那么图中与△ABC成轴对称且也以格点为顶点的三角形共有( )
如图所示,△ABC是在2×2的正方形网格中以格点为顶点的三角形,那么图中与△ABC成轴对称且也以格点为顶点的三角形共有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
1.某公司准备投资开发A、B两种新产品,信息部通过市场调研得到两条信息:
信息一:如果投资A种产品,所获利润yA(万元)与投资金额x(万元)之间满足正比例函数关系:y=kx;
信息二:如果投资B种产品,所获利润yB(万元)与投资金额x(万元)之间满足二次函数关系:yB=ax2+bx.
根据公司信息部报告,yA、yB(万元)与投资金额x(万元)的部分对应值如上表所示:
(1)填空:yA=0.6x; yB=-0.2x2+2.6x;
(2)如果公司准备投资15万元同时开发A、B两种新产品,设公司所获得的总利润为W(万元),B种产品的投资金额为x(万元),试求出W与x之间的函数关系式;
(3)请你设计一个在(2)中公司能获得最大总利润的投资方案.
| x(万元) | 1 | 2 |
| yA(万元) | 0.6 | 1.2 |
| yB(万元) | 2.4 | 4.4 |
信息二:如果投资B种产品,所获利润yB(万元)与投资金额x(万元)之间满足二次函数关系:yB=ax2+bx.
根据公司信息部报告,yA、yB(万元)与投资金额x(万元)的部分对应值如上表所示:
(1)填空:yA=0.6x; yB=-0.2x2+2.6x;
(2)如果公司准备投资15万元同时开发A、B两种新产品,设公司所获得的总利润为W(万元),B种产品的投资金额为x(万元),试求出W与x之间的函数关系式;
(3)请你设计一个在(2)中公司能获得最大总利润的投资方案.
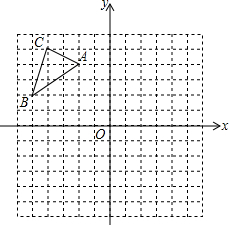 已知△ABC在平面直角坐标系中的位置如图所示.将△ABC向右平移6个单位长度,再向下平移4个单位长度得到△A1B1C1.(图中每个小方格边长均为1个单位长度)
已知△ABC在平面直角坐标系中的位置如图所示.将△ABC向右平移6个单位长度,再向下平移4个单位长度得到△A1B1C1.(图中每个小方格边长均为1个单位长度)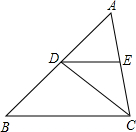 如图,CD平分∠ACB,DE∥BC,∠AED=80°,求∠ECD的度数.
如图,CD平分∠ACB,DE∥BC,∠AED=80°,求∠ECD的度数.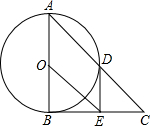 如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心,OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.
如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心,OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.