题目内容
18.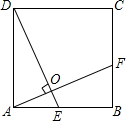 如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O,则$\frac{OE}{BF}$等于( )
如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O,则$\frac{OE}{BF}$等于( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{5}}{3}$ |
分析 由四边形ABCD是正方形,证得△ADE≌△BAF,进而证得BF=AE,利用两角对应相等易得△AOE∽△ABF,那么$\frac{OE}{BF}=\frac{AE}{AF}$ 问题得解.
解答 解:∵四边形ABCD是正方形,
∴AD=AB,∠DAB=∠B=90°,
∵DE⊥AF,
∴∠ADE+∠DAO=∠DAO+∠OAF=90°
∴∠ADE=∠OAE,
在△ADE和△BAF中,
$\left\{\begin{array}{l}{∠ADE=∠OAF}\\{AD=AB}\\{∠DAE=∠ABF}\end{array}\right.$,
∴△ADE≌△BAF,
∴BF=AE,
∵AE=$\frac{1}{2}$AB,
∴BF=$\frac{1}{2}$AB,
设BF=1,则AB=2,
∴AF=$\sqrt{5}$,
∵∠AOE=∠B=90°.
∠OAE=∠FAB,
∴△AOE∽△ABF,
∴$\frac{OE}{BF}=\frac{AE}{AF}=\frac{1}{\sqrt{5}}=\frac{\sqrt{5}}{5}$.
故选C.
点评 本题考查了正方形的性质,三角形全等的判定和相似三角形的判定与应用;把所求的线段的比进行相应的转移是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.菱形的一个内角是120°,一条较短的对角线的长为10,则菱形的周长是( )
| A. | 10 | B. | 20 | C. | 30 | D. | 40 |
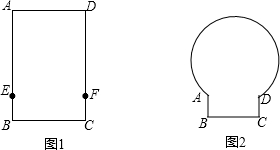
 如图,⊙O的直径AB=6,点C为⊙0外一点,CA、CB分别交⊙O于E、F,cos∠C=$\frac{2}{3}$,则EF的长为( )
如图,⊙O的直径AB=6,点C为⊙0外一点,CA、CB分别交⊙O于E、F,cos∠C=$\frac{2}{3}$,则EF的长为( ) 如图,点D、E分别在△ABC的边上AB、AC上,且∠ADC=∠ACB,若DE=4,AC=7,BC=8,AB=10,则AE的长为5.
如图,点D、E分别在△ABC的边上AB、AC上,且∠ADC=∠ACB,若DE=4,AC=7,BC=8,AB=10,则AE的长为5.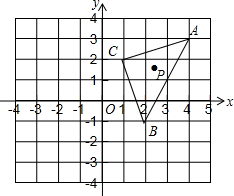 在平面直角坐标系中,△ABC的三个顶点的位置如图,P为△ABC内一点,P的坐标为(a,b).
在平面直角坐标系中,△ABC的三个顶点的位置如图,P为△ABC内一点,P的坐标为(a,b).