题目内容
19.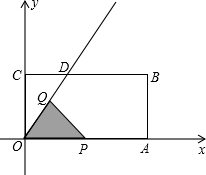 如图,已知矩形ABCD中,OA=8,AB=1,直线y=$\frac{4}{3}$x交BC于D,动点P、Q同时从D出发,点P沿折线OA-AB-BD以每秒3个单位的速度运动到D停止,点Q沿射线OD以每秒1个单位的速度运动,当点P停止时,点Q也停止运动.△OPQ与梯形OABD重叠部分的面积为S,运动时间为t.
如图,已知矩形ABCD中,OA=8,AB=1,直线y=$\frac{4}{3}$x交BC于D,动点P、Q同时从D出发,点P沿折线OA-AB-BD以每秒3个单位的速度运动到D停止,点Q沿射线OD以每秒1个单位的速度运动,当点P停止时,点Q也停止运动.△OPQ与梯形OABD重叠部分的面积为S,运动时间为t.(1)求D的坐标;
(2)写出面积S与时间t的函数关系式;
(3)t为何值时,S有最大值,并求出最大值.
分析 (1)把y=1代入直线OD解析式求出x的值,确定出D坐标即可;
(2)分两种情况考虑:若Q在线段OD上时;若Q到D停止时,分别表示出S与t的函数解析式即可;
(3)当Q在D处停止,P在A处停止时,△OPQ与梯形OABD重叠部分的面积为△AOD,面积最大,求出即可.
解答 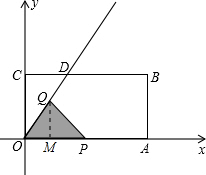 解:(1)把y=1代入y=$\frac{4}{3}$x,得:x=$\frac{3}{4}$,
解:(1)把y=1代入y=$\frac{4}{3}$x,得:x=$\frac{3}{4}$,
则D($\frac{3}{4}$,1);
(2)分两种情况考虑:
若Q在线段OD上时,过Q作QM⊥OP,
在Rt△OQM中,OQ=t,OP=3t,
∵tan∠QOM=$\frac{QM}{OM}$=$\frac{4}{3}$,即QM=4a,OM=3a,
∴OQ=5a=t,即a=$\frac{t}{5}$,
∴QM=$\frac{4}{5}$t,
∴S=$\frac{1}{2}$OP•QM=$\frac{1}{2}$×3t×$\frac{4}{5}$t=$\frac{6}{5}$t2(0≤t<$\frac{5}{4}$);
若Q到D停止时,S=$\frac{1}{2}$×3t×1=$\frac{3}{2}$t($\frac{5}{4}$≤t≤$\frac{8}{3}$);
(3)当t=$\frac{8}{3}$时,S有最大值,最大值为$\frac{1}{2}$×1×8=4.
点评 此题属于一次函数综合题,涉及的知识有:坐标与图形性质,一次函数、二次函数的性质,锐角三角函数定义,熟练掌握一次函数的性质是解本题的关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
10.菱形的一个内角是120°,一条较短的对角线的长为10,则菱形的周长是( )
| A. | 10 | B. | 20 | C. | 30 | D. | 40 |
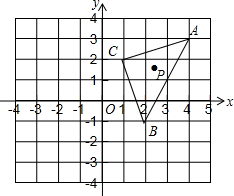 在平面直角坐标系中,△ABC的三个顶点的位置如图,P为△ABC内一点,P的坐标为(a,b).
在平面直角坐标系中,△ABC的三个顶点的位置如图,P为△ABC内一点,P的坐标为(a,b). 如图,在下面的网络图中,按要求画出图形,并回答问题:
如图,在下面的网络图中,按要求画出图形,并回答问题: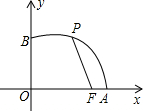 如图,已知点F的坐标为(3,0),点A、B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点,设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}$x(0≤x≤5),则结论:①AF=2;②BF=4;③OA=5;④OB=3,正确结论的序号是( )
如图,已知点F的坐标为(3,0),点A、B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点,设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-$\frac{3}{5}$x(0≤x≤5),则结论:①AF=2;②BF=4;③OA=5;④OB=3,正确结论的序号是( ) 如图,二次函数y=-$\frac{\sqrt{3}}{3}{x}^{2}-\frac{2}{3}\sqrt{3}x+\sqrt{3}$的图象交x轴于A,B两点,交y轴于点C,顶点为D.
如图,二次函数y=-$\frac{\sqrt{3}}{3}{x}^{2}-\frac{2}{3}\sqrt{3}x+\sqrt{3}$的图象交x轴于A,B两点,交y轴于点C,顶点为D.
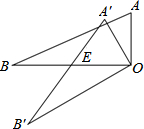 如图,△AOB中,∠AOB=90°,AO=3,BO=6,△AOB绕顶点O逆时针旋转到△AOB处,此时线段A′B′与BO的交点E为BO的中点,则线段B′E的长度为$\frac{9\sqrt{5}}{5}$.
如图,△AOB中,∠AOB=90°,AO=3,BO=6,△AOB绕顶点O逆时针旋转到△AOB处,此时线段A′B′与BO的交点E为BO的中点,则线段B′E的长度为$\frac{9\sqrt{5}}{5}$.