题目内容
7. 如图,P是正三角形ABC内的一点,若将△PAC绕点A逆时针旋转后,得到△P′AB,
如图,P是正三角形ABC内的一点,若将△PAC绕点A逆时针旋转后,得到△P′AB,(1)若PA=1,PB=$\sqrt{3}$,PC=2,则点P与点P′之间的距离为1,∠APB=150°.
(2)若∠CPB=110°,∠APC=α,则当α为140°或65°或110°度时,△P′PB是等腰三角形.
分析 (1)由已知△PAC绕点A逆时针旋转后,得到△P′AB,可得△PAC≌△P′AB,PA=P′A,旋转角∠P′AP=∠BAC=60°,所以△APP′为等边三角形,即可求得PP′;再由△APP′为等边三角形,得∠APP′=60°,在△PP′B中,已知三边,用勾股定理逆定理证出直角三角形,得出∠P′PB=90°,可求∠APB的度数.
(2)根据旋转的性质得出△P′PA是等边三角形,得出∠P′PA=∠PP′A=60°,设∠APC=x时,由△BPP′是等腰三角形,则∠BP′A=x,∠BP′P=x-60°,分三种情况分别讨论求得∠BPP′的值,根据∠BPP′+∠P′PA+∠BPC+∠BPC=360°,列出等式即可求得.
解答 解:(1)由题意可知BP′=PC=2,AP′=AP,
∠PAC=∠P′AB,而∠PAC+∠BAP=60°,
所以∠PAP′=60度.故△APP′为等边三角形,
所以PP′=AP=AP′=1;
∵PA=1,PB=$\sqrt{3}$,PC=2.
∴PP′2+BP2=BP′2,
∴△BPP′为直角三角形,且∠BPP′=90°
∴∠APB=90°+60°=150°.
(2)∵PA=P′A,∠PAP′=60°,
∴△P′PA是等边三角形,
∴∠P′PA=∠PP′A=60°,
设∠APC=x时,由△BPP′是等腰三角形,则∠AP′B=x,
∴∠BP′P=x-60°,
①当P′B=P′P时,则∠P′PB=∠PBP′=$\frac{180°-(x-60°)}{2}$,
∵∠BPP′+∠P′PA+∠APC+∠BPC=360°,
∴$\frac{180°-(x-60°)}{2}$+60°+x+110°=360°,
解得x=140°;
②当P′B=BA时,则∠P′PB=∠PP′B=x-60°
∵∠BPP′+∠P′PA+∠APC+∠BPC=360°,
∴x-60°+60°+x+110°=360°,
解得x=65°;
③当P′P=PB时,则∠P′PB=180°-2(x-60°)=300°-2x
∵∠BPP′+∠P′PA+∠APC+∠BPC=360°,
∴300°-2x+60°+x+110°=360°,
解得x=110°;
所以,当∠APC为140°或65°或110°,△BPP′是等腰三角形.
故答案为:1,150°;140°或65°或110°.
点评 本题考查了旋转的性质以及等边三角形的判定与性质和勾股定理的逆定理,注意:旋转图形的性质:旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案| A. | 2a+3b=5ab | B. | 3x2÷2x=x | C. | (x2)3=x6 | D. | (x+y2)2=x2+y4 |
| A. | $\sqrt{3}$ | B. | 0 | C. | -1 | D. | $\sqrt{9}$ |
 如图,梯形ABCD中,AD∥BC,E是CD的中点,AE平分∠BAD,AE⊥BE.
如图,梯形ABCD中,AD∥BC,E是CD的中点,AE平分∠BAD,AE⊥BE.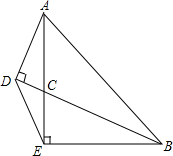 如图,△ABE中,∠AEB=90°,AE=BE,BC平分∠ABE交AE于C,AD⊥BC于D,连DE.
如图,△ABE中,∠AEB=90°,AE=BE,BC平分∠ABE交AE于C,AD⊥BC于D,连DE.