题目内容
5.方程组$\left\{\begin{array}{l}{x-y=3}\\{x+2y=a-3}\end{array}\right.$的解x、y的和为负数,则a的取值范围是a<$\frac{3}{2}$.分析 解关于x、y的二元一次方程组,根据x、y的和为负数得到关于a的不等式,解不等式可得a的范围.
解答 解:解方程组$\left\{\begin{array}{l}{x-y=3}&{①}\\{x+2y=a-3}&{②}\end{array}\right.$,
②-①,得:3y=a-6,解得:y=$\frac{a-6}{3}$,
将y=$\frac{a-6}{3}$代入①,得:x-$\frac{a-6}{3}$=3,解得:x=$\frac{a+3}{3}$,
∵x、y的和为负数,
∴$\frac{a-6}{3}$+$\frac{a+3}{3}$<0,
解得:a<$\frac{3}{2}$,
故答案为:a<$\frac{3}{2}$.
点评 本题主要考查解二元一次方程组的能力与二元一次方程组的解,根据题意得出关于a的一元一次不等式是解题的关键.

练习册系列答案
相关题目
15.下列命题中,正确的有( )
①过一点有且只有一条直线与已知直线平行;②若a∥b,b∥c,则a∥c;③两条直线被第三条直线所截,同位角相等;④邻补角的平分线互相垂直.
①过一点有且只有一条直线与已知直线平行;②若a∥b,b∥c,则a∥c;③两条直线被第三条直线所截,同位角相等;④邻补角的平分线互相垂直.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
16. 如图,函数y=kx和y=-$\frac{1}{2}$x+4的图象相交于点A(m,3),则不等式kx≥-$\frac{1}{2}$x+4的解集为 ( )
如图,函数y=kx和y=-$\frac{1}{2}$x+4的图象相交于点A(m,3),则不等式kx≥-$\frac{1}{2}$x+4的解集为 ( )
 如图,函数y=kx和y=-$\frac{1}{2}$x+4的图象相交于点A(m,3),则不等式kx≥-$\frac{1}{2}$x+4的解集为 ( )
如图,函数y=kx和y=-$\frac{1}{2}$x+4的图象相交于点A(m,3),则不等式kx≥-$\frac{1}{2}$x+4的解集为 ( )| A. | x≥3 | B. | x≤3 | C. | x≤2 | D. | x≥2 |
20.下列命题中,是真命题的是( )
| A. | 经过直线外一点,有且只有一条直线与这条直线平行 | |
| B. | 两条直线被第三条直线所截,同位角相等 | |
| C. | 相等的两个角是对顶角 | |
| D. | 从直线外一点到这条直线的垂线段,叫做这点到直线的距离 |
10. 如图,把一块三角板的直角顶点放在直尺的一边上,如果∠1=30°,那么∠2为( )
如图,把一块三角板的直角顶点放在直尺的一边上,如果∠1=30°,那么∠2为( )
 如图,把一块三角板的直角顶点放在直尺的一边上,如果∠1=30°,那么∠2为( )
如图,把一块三角板的直角顶点放在直尺的一边上,如果∠1=30°,那么∠2为( )| A. | 60° | B. | 30° | C. | 70° | D. | 50° |
17.下列正多边形的组合中,能够铺满地面的是( )
| A. | 正六边形和正方形 | B. | 正五边形和正八边形 | ||
| C. | 正六边形和正三角形 | D. | 正十边形和正三角形 |
14.点到直线的距离是( )
| A. | 直线外一点与这条直线上任意一点的距离 | |
| B. | 直线外一点到这条直线的垂线的长度 | |
| C. | 直线外一点到这条直线的垂线段 | |
| D. | 直线外一点到这条直线的垂线段的长度 |
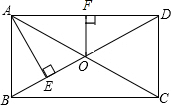 如图,在矩形ABCD中,对角线AC、BD交于点O,自点A作AE⊥BD于点E,且BE:ED=1:3,过点O作OF⊥AD于点F,若OF=3cm,则BD的长为( )cm.
如图,在矩形ABCD中,对角线AC、BD交于点O,自点A作AE⊥BD于点E,且BE:ED=1:3,过点O作OF⊥AD于点F,若OF=3cm,则BD的长为( )cm.