如图.⊙O的直径CD垂直于弦AB.∠AOC=40°.则∠CDB的度数为( )A．40°B．30°C．20°D．10° 题目和参考答案——青夏教育精英家教网—

题目内容

11．

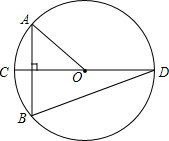如图，⊙O的直径CD垂直于弦AB，∠AOC=40°，则∠CDB的度数为（　　）

A．

40°

B．

30°

C．

20°

D．

10°

分析由⊙O的直径CD垂直于弦AB，根据垂径定理，可得$\widehat{AC}$=$\widehat{BC}$，然后由在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半，即可求得答案．

解答解：∵⊙O的直径CD垂直于弦AB，
∴$\widehat{AC}$=$\widehat{BC}$，
∴∠CDB=$\frac{1}{2}$∠AOC=$\frac{1}{2}$×40°=20°．
故选C．

点评此题考查了圆周角定理以及垂径定理．注意掌握在同圆或等圆中，同弧或等弧所对的圆周角相都等于这条弧所对的圆心角的一半是关键．

练习册系列答案

相关题目

1．多项式x²+mx-12因式分解可得（x+4）（x+n），则mn的值为-3．

2．等腰三角形的一个外角等于130°，则这个等腰三角形的底角为（　　）

19．

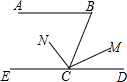如图，已知AB∥CD，CN是∠BCE的平分线．
（1）若CM平分∠BCD，求∠MCN的度数；
（2）若CM在∠BCD的内部，且CM⊥CN于C，求证：CM平分∠BCD；
（3）在（2）的条件下，连结BM、BN，且BM⊥BN，∠MBN绕着B点旋转，∠BMC+∠BNC是否发生变化？若不变，求其值；若变化，求其变化范围．

6．已知直线AB∥CD，点E在直线AB上，点EG在直线CD上，∠EFC、∠EGD的平分线FM、GN分别交直线AB于M、N．
（1）如果△EFG为等边三角形（如图1），那么∠1+∠2=120°．如果△EFG为等腰三角形（如图2），且顶角∠FEG=36°，那么∠1+∠2=108°．
（2）如果△EFG为任意三角形（如图3），那么∠1+∠2与∠FEG有什么关系？试说明理由；
（3）当三角形的一个内角α是另一个内角β的两倍时，我们称此三角形为“倍角三角形”，其中α为“倍角”，如果△EFG是有一个角为30°的“倍角三角形”，且∠FEG为“倍角”，请利用（2）中的结论求∠1+∠2的度数．

16．

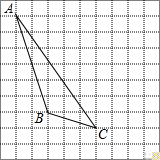如图，在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′．
（1）补全△A′B′C′，利用网格点和直尺画图；
（2）图中AC与A₁C₁的关系是：平行且相等；
（3）画出AB边上的高线CD；
（4）画出△ABC中AB边上的中线CE；
（5）△BCE的面积为4．

3．

墨墨对他所住小区的100户居民2月份天然气的使用量（单位：m³）进行统计，其结果如图所示，图中36-38段因不小心洒上水而看不清，则2月份天然气的使用量在36-38段的居民有（　　）

20．

如图，在△ABC中点D、E分别在边AB、AC上，请添加一个条件：∠AEB=∠B（答案不唯一），使△ABC∽△AED．

1．

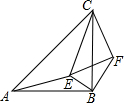如图，△ABC和△CEF均为等腰直角三角形，E在△ABC内，∠CAE+∠CBE=90°，连接BF．
（1）求证：△CAE∽△CBF．
（2）若BE=1，AE=2，求CE的长．

试题分类