题目内容
5.当0<x<2时,化简:$\sqrt{\frac{{x}^{2}+4}{2x}+2}$+$\sqrt{\frac{{x}^{2}+4}{2x}-2}$.分析 结合二次根式的性质进行化简求值即可.
解答 解:$\sqrt{\frac{{x}^{2}+4}{2x}+2}$+$\sqrt{\frac{{x}^{2}+4}{2x}-2}$
=$\sqrt{\frac{{x}^{2}+4+4x}{2x}}$+$\sqrt{\frac{{x}^{2}+4-4x}{2x}}$
=$\sqrt{\frac{(x+2)^{2}}{2x}}$+$\sqrt{\frac{(x-2)^{2}}{2x}}$
=$\frac{|x+2|}{\sqrt{2x}}$+$\frac{|x-2|}{\sqrt{2x}}$,
∵0<x<2,
∴x+2>0,x-2<0,
∴原式=$\frac{|x+2|}{\sqrt{2x}}$+$\frac{|x-2|}{\sqrt{2x}}$
=$\frac{x+2}{\sqrt{2x}}$+$\frac{2-x}{\sqrt{2x}}$
=$\frac{4}{\sqrt{2x}}$
=$\frac{2\sqrt{2x}}{x}$.
点评 本题考查了二次根式的性质与化简,解答本题的关键在于熟练二次根式的性质及绝对值的化简.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
15.若5x2-3xy+y2与一个多项式的和是3xy-x2,则这个多项式是( )
| A. | 6x2-3xy+y2 | B. | -6x2+6xy-y2 | C. | 4x2+y2 | D. | -6x+y2 |
16.已知一个等腰三角形的腰长,底边长满足x2+y2-6x-12y+45=0,则这个等腰三角形的周长是( )
| A. | 12 | B. | 15 | C. | 12或15 | D. | 45 |
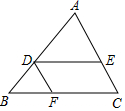 在△ABC中,D,E、F分别在AB、AC、BC上,已知:$\frac{AD}{DB}$=$\frac{AE}{DF}$=$\frac{DE}{BF}$,求证:四边形CFDE是平行四边形.
在△ABC中,D,E、F分别在AB、AC、BC上,已知:$\frac{AD}{DB}$=$\frac{AE}{DF}$=$\frac{DE}{BF}$,求证:四边形CFDE是平行四边形.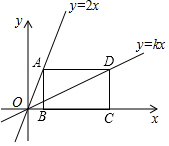 如图,在长方形ABCD中,AB=2,BC=3,点B,C均在x轴上,点A,D分别是直线y=2x和y=kx上,求k的值.
如图,在长方形ABCD中,AB=2,BC=3,点B,C均在x轴上,点A,D分别是直线y=2x和y=kx上,求k的值.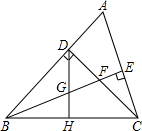 已知,如图△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连接DH与BE相交于点G,有如下四个结论:①BF=AC;②CE=$\frac{1}{2}$BF;③CE>BG;④DG=DF;⑤连接DE,则∠DEB=45°,其中正确的有( )
已知,如图△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连接DH与BE相交于点G,有如下四个结论:①BF=AC;②CE=$\frac{1}{2}$BF;③CE>BG;④DG=DF;⑤连接DE,则∠DEB=45°,其中正确的有( )