题目内容
17．
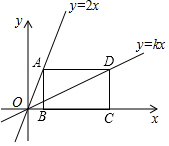如图，在长方形ABCD中，AB=2，BC=3，点B，C均在x轴上，点A，D分别是直线y=2x和y=kx上，求k的值．
分析 根据长方形ABCD的边长可得出A点纵坐标，代入y=2x可求得A点的坐标，然后可得出D点的坐标，将D点的坐标代入y=kx，即可求出k的值．
解答 解：∵在长方形ABCD中，AB=2，BC=3，A点的纵坐标是2，
把点A的纵坐标代入直线y=2x的解析式得：x=1，
则点A的坐标为（1，2），点D的坐标为（4，2），
把点D的坐标代入y=kx中得，2=4k，
解得：k=$\frac{1}{2}$．
点评 本题考查了一次函数与矩形的结合，解答本题的关键是根据矩形的性质得出点D的坐标，利用待定系数法确定k，难度一般．
练习册系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
相关题目
12．已知：角α的终边经过点（$\frac{1}{2}$，-$\frac{\sqrt{2}}{2}$），则tanα=（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{\sqrt{6}}{3}$ | C． | -$\frac{\sqrt{3}}{2}$ | D． | -$\sqrt{2}$ |