题目内容
13．先化简，再求值：（1+$\frac{1}{x}$）÷$\frac{{x}^{2}+2x+1}{x}$，其中x满足x2-x-2=0．分析 先根据分式的混合运算化简分式，再利用因式分解法解方程求得x的值，最后代入求解可得．
解答 解：原式=$\frac{x+1}{x}$•$\frac{x}{（x+1）^{2}}$=$\frac{1}{x+1}$，
∵x2-x-2=0，
∴（x+1）（x-2）=0，
∴x+1=0或x-2=0，
解得：x=-1（舍）或x=2，
当x=2时，原式=$\frac{1}{3}$．
点评 本题主要考查分式的化简求值及解一元二次方程的能力，熟练掌握分式的运算顺序和法则及解方程的基本方法是解题的关键．
练习册系列答案
相关题目
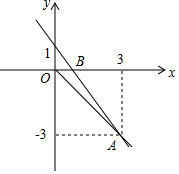函数y=kx+1的图象经过点A（3，-3），且与x轴相交于B点，O为坐标原点．
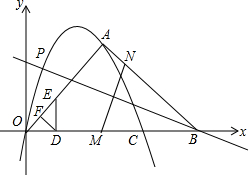如图，二次函数y=-$\frac{1}{2}$x2+$\frac{7}{2}$x的图象与x轴交于O、C两点，点A在抛物线上，坐标为（5，a），点P是该抛物线位于x轴上方的动点，过点P的直线y=kx-$\frac{35}{3}$k（k≠0）交x轴于点B，连接OA、BA．