题目内容
9.计算:(1)$\sqrt{2}$×$\sqrt{32}$+($\sqrt{2}$-1)2
(2)$\frac{x}{x^2-4}$-$\frac{1}{2x-4}$
(3)解方程:$\frac{2x+9}{3x-9}$=$\frac{4x-7}{x-3}$+2.
分析 (1)利用二次根式的乘法法则和完全平方公式计算;
(2)先把分母化为同分母,再进行同分母的减法运算,然后约分即可;
(3)先去分母化为整式方程2x+9=3(4x-7)+2(3x-9),再解一元一次方程,然后检验确定原方程的解.
解答 解:(1)原式=$\sqrt{2×32}$+2-2$\sqrt{2}$+1
=8+3-2$\sqrt{2}$
=11-2$\sqrt{2}$;
(2)原式=$\frac{x}{(x+2)(x-2)}$-$\frac{1}{2(x-2)}$
=$\frac{2x-(x+2)}{2(x+2)(x-2)}$
=$\frac{1}{2x+4}$;
(3)2x+9=3(4x-7)+2(3x-9),
2x+9=12x-21+6x-18,
2x-12x-6x=-21-18-9,
-16x=-48,
所以x=3,
检验:当x=3时,x-3=0,则x=3是原方程的增根,
所以原方程无解.
点评 本题考查了二次根式的混合运算:先把各二次根式化简为最简二次根式,然后进行二次根式的乘除运算,再合并即可.也考查了解分式方程.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
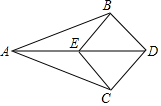 如图,已知AD平分∠BAC,且∠ABD=∠ACD,则由“AAS“可直接判定△ABD≌△ACD.
如图,已知AD平分∠BAC,且∠ABD=∠ACD,则由“AAS“可直接判定△ABD≌△ACD.