题目内容
14.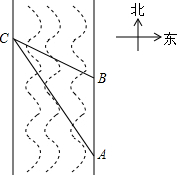 在一次数学实验活动中,老师带领学生去测一条南北流向的河的宽度.如图,某同学在河东岸点A处观测河对岸水边有点C,测得C在A北偏西31°的方向上,沿河岸向北前行20米到达B处,测得C在B北偏西45°的方向上,则这条河的宽度30米.(参考数据:$tan31°=\frac{3}{5},sin31°≈\frac{1}{2}$)
在一次数学实验活动中,老师带领学生去测一条南北流向的河的宽度.如图,某同学在河东岸点A处观测河对岸水边有点C,测得C在A北偏西31°的方向上,沿河岸向北前行20米到达B处,测得C在B北偏西45°的方向上,则这条河的宽度30米.(参考数据:$tan31°=\frac{3}{5},sin31°≈\frac{1}{2}$)
分析 作CE⊥AB于E,设CE=x,在RT△ACE中,根据tan∠CAE=$\frac{CE}{AE}$=$\frac{3}{5}$列出方程即可解决问题.
解答 解: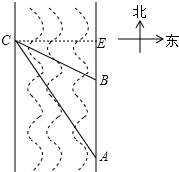 如图,作CE⊥AB于E,
如图,作CE⊥AB于E,
设CE=x,
由题意得∠CBE=45°,∠CAE=31°,
∴∠CBE=∠BCE=45°,
∴CE=BE=x,AE=20+x,
∵tan31°=$\frac{CE}{AE}$=$\frac{3}{5}$,
∴$\frac{x}{20+x}$=$\frac{3}{5}$,
∴x=30,
∴CE=30米.
故答案为30.
点评 本题考查解直角三角形、方向角、三角函数等知识,解题的关键是添加辅助线构造直角三角形,学会利用方程解决问题,属于中考常考题型.

练习册系列答案
相关题目
5.下列图形中,是中心对称图形,但不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
9.济南市名校德润中学九年级学生去距学校10千米的博物馆参观,一部分学生骑自行车先走,过了$\frac{1}{3}$小时后,其余学生乘汽车出发,结果他们同时达到,已知乘汽车学生的速度是骑车学生速度的2倍,求骑车学生的速度.设骑车学生的速度为每小时x千米,则所列方程正确的是( )
| A. | $\frac{10}{x}=\frac{10}{2x}+\frac{1}{3}$ | B. | $\frac{10}{2x}=\frac{10}{x}+\frac{1}{3}$ | C. | $\frac{10}{x}=\frac{1}{3}-\frac{10}{2x}$ | D. | $\frac{10}{2x}-\frac{1}{3}=\frac{10}{x}$ |
 在平面直角坐标系中,顺次连结点A(-2,0)、B(0,-2)、C(2,0)、D(0,2)所得的四边形ABCD是怎样的四边形?并说明理由.
在平面直角坐标系中,顺次连结点A(-2,0)、B(0,-2)、C(2,0)、D(0,2)所得的四边形ABCD是怎样的四边形?并说明理由.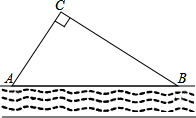 某校生物兴趣小组把一块沿河的三角形废地(如图)开辟为生物园(设AB段河岸为直线),已知∠ACB=90°,∠CAB=55°,BC=80米,学校决定在点C处建一个蓄水池,利用管道从河中取水,已知每铺设1米管道费用为50元,求铺设管道的最低费用(精确到1元).(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
某校生物兴趣小组把一块沿河的三角形废地(如图)开辟为生物园(设AB段河岸为直线),已知∠ACB=90°,∠CAB=55°,BC=80米,学校决定在点C处建一个蓄水池,利用管道从河中取水,已知每铺设1米管道费用为50元,求铺设管道的最低费用(精确到1元).(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)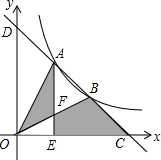 如图,一次函数y=-x+b与反比例函数y=$\frac{4}{x}$(x>0)的图象交于A,B两点,与x轴、y轴分别交于C,D两点,连结OA,OB,过A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m.
如图,一次函数y=-x+b与反比例函数y=$\frac{4}{x}$(x>0)的图象交于A,B两点,与x轴、y轴分别交于C,D两点,连结OA,OB,过A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m.