题目内容
19．在学校组织的数学实践活动中，小新同学制作了一个圆锥模型，它的底面半径为1，高为2$\sqrt{2}$，则这个圆锥的侧面积是3π．分析 先利用勾股定理计算出圆锥的高，然后利用圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和扇形的面积公式计算这个圆锥的侧面积．
解答 解：圆锥的母线长=$\sqrt{（2\sqrt{2}）^{2}+{1}^{2}}$=3，
所以这个圆锥的侧面积=$\frac{1}{2}$•2π•1•3=3π．
故答案为3π．
点评 本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
如图所示，在平面直角坐标系中，点A，B的坐标分别为A（a，0），B（b，0），且a，b满足|a+2|+$\sqrt{b-4}$=0，点C的坐标为（0，3）．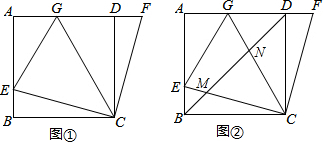
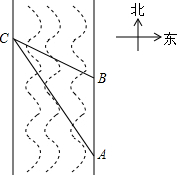在一次数学实验活动中，老师带领学生去测一条南北流向的河的宽度．如图，某同学在河东岸点A处观测河对岸水边有点C，测得C在A北偏西31°的方向上，沿河岸向北前行20米到达B处，测得C在B北偏西45°的方向上，则这条河的宽度30米．（参考数据：$tan31°=\frac{3}{5}，sin31°≈\frac{1}{2}$）
4．
如图是一个正方体的表面展开图，则原正方体标有数字“1”所在面的对面标有数字（ ）
如图是一个正方体的表面展开图，则原正方体标有数字“1”所在面的对面标有数字（ ）| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
如图，一个书架上的方格中放着四本厚度和长度相同的书，其中左边两边上紧贴书架方格内侧竖放，右边两本书自然向左斜放，支撑点为C，E，右侧书角正好靠在方格内侧上，若书架方格长BF=40cm，∠DCE=30°．
如图，用一个半径为30cm，面积为300πcm2的扇形铁皮，制作一个无底的圆锥（不计损耗），圆锥的底面半径r，高为h，则高h为20$\sqrt{2}$cm．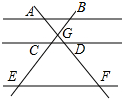
如图，AB∥CD∥EF，AF与BE相交于点G，且AG=2，GD=1，DF=5，那么$\frac{BC}{CE}$的值等于$\frac{3}{5}$．