题目内容
2. 在平面直角坐标系中,顺次连结点A(-2,0)、B(0,-2)、C(2,0)、D(0,2)所得的四边形ABCD是怎样的四边形?并说明理由.
在平面直角坐标系中,顺次连结点A(-2,0)、B(0,-2)、C(2,0)、D(0,2)所得的四边形ABCD是怎样的四边形?并说明理由.
分析 由A、B、C、D四点坐标结合两点间的距离公式可得出线段AD=BC=2$\sqrt{2}$,OA=OB=OC=OD=2,再由正切的定义得出tan∠DAO=tan∠BCO=1,由此得出∠DAO=∠BCO=45°,同理可得出∠BAO=∠DCO=45°,由角相等利用“内错角相等,两直线平行”可得出AD∥BC,由此即可得知四边形ABCD是平行四边形,再根据角的计算得出∠DAB=90°即可证出四边形ABCD是正方形.
解答 解:所得的四边形ABCD是正方形,理由如下:
∵点A(-2,0)、B(0,-2)、C(2,0)、D(0,2),
∴AD=$\sqrt{(-2-0)^{2}+(0-2)^{2}}$=2$\sqrt{2}$,BC=$\sqrt{(0-2)^{2}+(-2-0)^{2}}$=2$\sqrt{2}$,OA=OB=OC=OD=2,
∴tan∠DAO=$\frac{OD}{OA}$=1,tan∠BCO=$\frac{OB}{OC}$=1,
∴tan∠DAO=tan∠BCO,即∠DAO=∠BCO=45°,
同理可得∠BAO=∠DCO=45°.
∵∠DAO=∠BCO,
∴AD∥BC,
∴四边形ABCD是平行四边形.
同理可得∠BAO=∠DCO=45°,
∵∠DAB=∠DAO+∠BAO=90°,
∴四边形ABCD是正方形.
点评 本题考查了坐标与图形性质、两点间的距离公式、正切的定义以及正方形的判定定理,解题的关键是利用正方形的判定定理证明四边形ABCD是正方形.本题属于基础题,难度不大,解决该题型题目时,根据点的坐标结合两点间的距离公式以及角的计算找出平行且相等的量以及含有90°的内角,再根据正方形的判定定理证明四边形为正方形即可.

练习册系列答案
相关题目
12.若x,y都是实数,且$\sqrt{2x-1}$+$\sqrt{2-4x}$+y=4,则xy的值是( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | 2 | D. | 不能确定 |
13.计算-5+2的结果是( )
| A. | -7 | B. | -3 | C. | 3 | D. | 7 |
12. 一物体的左视图和俯视图如图所示,则其主视图为( )
一物体的左视图和俯视图如图所示,则其主视图为( )
 一物体的左视图和俯视图如图所示,则其主视图为( )
一物体的左视图和俯视图如图所示,则其主视图为( )| A. |  | B. |  | C. |  | D. |  |
 如图所示,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|a+2|+$\sqrt{b-4}$=0,点C的坐标为(0,3).
如图所示,在平面直角坐标系中,点A,B的坐标分别为A(a,0),B(b,0),且a,b满足|a+2|+$\sqrt{b-4}$=0,点C的坐标为(0,3). 如图,某居民小区有一栋居民楼,在该楼的前面32米处要再盖一栋30米的新楼,现需了解新楼对采光的影响,当冬季正午的阳光与水平线的夹角为37°时,求新楼的影子在居民楼上有多高?
如图,某居民小区有一栋居民楼,在该楼的前面32米处要再盖一栋30米的新楼,现需了解新楼对采光的影响,当冬季正午的阳光与水平线的夹角为37°时,求新楼的影子在居民楼上有多高?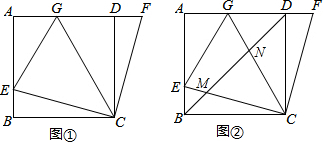
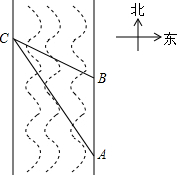 在一次数学实验活动中,老师带领学生去测一条南北流向的河的宽度.如图,某同学在河东岸点A处观测河对岸水边有点C,测得C在A北偏西31°的方向上,沿河岸向北前行20米到达B处,测得C在B北偏西45°的方向上,则这条河的宽度30米.(参考数据:$tan31°=\frac{3}{5},sin31°≈\frac{1}{2}$)
在一次数学实验活动中,老师带领学生去测一条南北流向的河的宽度.如图,某同学在河东岸点A处观测河对岸水边有点C,测得C在A北偏西31°的方向上,沿河岸向北前行20米到达B处,测得C在B北偏西45°的方向上,则这条河的宽度30米.(参考数据:$tan31°=\frac{3}{5},sin31°≈\frac{1}{2}$) 如图,一个书架上的方格中放着四本厚度和长度相同的书,其中左边两边上紧贴书架方格内侧竖放,右边两本书自然向左斜放,支撑点为C,E,右侧书角正好靠在方格内侧上,若书架方格长BF=40cm,∠DCE=30°.
如图,一个书架上的方格中放着四本厚度和长度相同的书,其中左边两边上紧贴书架方格内侧竖放,右边两本书自然向左斜放,支撑点为C,E,右侧书角正好靠在方格内侧上,若书架方格长BF=40cm,∠DCE=30°.