题目内容
15.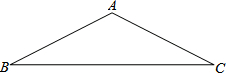 在△ABC中,AB=AC
在△ABC中,AB=AC(1)在图上分别画出AB,AC边上的高CF和BE;
(2)填充:S△ABC=$\frac{1}{2}$AC×BE,S△ABC=$\frac{1}{2}$AB×CF;
(3)比较:BE=CF;
(4)由此可以得到结论:等腰三角形两腰上的高相等.
分析 (1)分别过点BC向CA及BA的延长线作垂线,垂足分别为E、F;
(2)根据三角形的面积公式即可得出结论;
(3)根据AB=AC可得出结论;
(4)由(3)可得出结论.
解答  解:(1)如图,线段BE,CF即为所求;
解:(1)如图,线段BE,CF即为所求;
(2)∵BE⊥AC,CF⊥AB,
∴S△ABC=$\frac{1}{2}$AC•BE,S△ABC=$\frac{1}{2}$AB•CF.
故答案为:BE,CF;
(3)∵AB=AC,
∴BE=CF.
故答案为:=;
(4)由(3)可知,等腰三角形两腰上的高相等.
故答案为:等腰三角形两腰上的高相等.
点评 本题考查的是作图-基本作图,熟知等腰三角形的性质是解答此题的关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
4.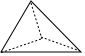 甲同学做抛正四面体骰子(如图:均匀的正四面体形状,各面分别标有数字1、2、3、4)实验,共抛了60次,向下面数字出现的次数如表:
甲同学做抛正四面体骰子(如图:均匀的正四面体形状,各面分别标有数字1、2、3、4)实验,共抛了60次,向下面数字出现的次数如表:
(1)计算此次实验中出现向下面数字为4的频率;
(2)如果甲、乙两同学各抛一枚这样的骰子,请用表格或树状图表示:两枚骰子向下面数字之和的所有等可能性结果,并求出和为3的倍数的概率.
 甲同学做抛正四面体骰子(如图:均匀的正四面体形状,各面分别标有数字1、2、3、4)实验,共抛了60次,向下面数字出现的次数如表:
甲同学做抛正四面体骰子(如图:均匀的正四面体形状,各面分别标有数字1、2、3、4)实验,共抛了60次,向下面数字出现的次数如表:| 向下面数字 | 1 | 2 | 3 | 4 |
| 出现次数 | 11 | 16 | 18 | 15 |
(2)如果甲、乙两同学各抛一枚这样的骰子,请用表格或树状图表示:两枚骰子向下面数字之和的所有等可能性结果,并求出和为3的倍数的概率.
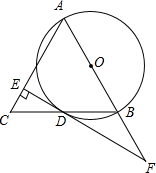 如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB的延长线于点F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB的延长线于点F.