题目内容
2.现有长144cm的铁丝,要截成n小段(n>2),每段的长度为不小于1cm的整数,如果其中任意三小段都不能拼成三角形,则n的最大值为10.分析 因n段之和为定值144cm,故欲n尽可能的大,必须每段的长度尽可能小,这样依题意可构造一个数列.
解答 解:∵每段的长为不小于1(cm)的整数,
∴最小的边最小是1,
∵三条线段不能构成三角形,则第二段是1,第三段是2,第四段与第二、第三段不能构成三角形,则第四边最小是3,第五边是5,依次是8,13,21,34,55,
再大时,各个小段的和大于150cm,不满足条件.
上述这些数之和为143,与144相差1,故可取1,1,2,3,5,8,13,21,34,56,
这时n的值最大,n=10.
故答案为:10
点评 本题考查了三角形三边关系,难度较大,解答本题的关键是保证前两项最短的情况下,使第三项等于前两项之和,这样便不能构成三角形.

练习册系列答案
相关题目
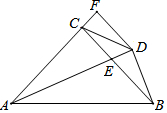 如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于 D,DF⊥AC交AC的延长线于F,连接CD,给出四个结论:
如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于 D,DF⊥AC交AC的延长线于F,连接CD,给出四个结论: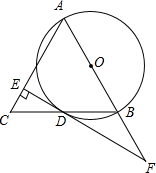 如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB的延长线于点F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作EF⊥AC于点E,交AB的延长线于点F.