题目内容
7.若一次函数y=kx+2的图象与反比例函数y=$\frac{1}{x}$的图象有两个公共点,则实数k的取值范围是k>-1且k≠0.分析 先由两解析式组成方程组,消去y得到关于x的一元二次方程kx2+2x-1=0,根据题意得到此方程有两个不相等的实数根,则△=22+4k>0,然后解不等式即可求解.
解答 解:由$\left\{\begin{array}{l}{y=kx+2}\\{y=\frac{1}{x}}\end{array}\right.$得kx+2=$\frac{1}{x}$,
整理得kx2+2x-1=0,
∵图象有两个公共点,
∴△=22+4k>0,
∴k>-1.
故答案为k>-1且k≠0.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
15.某市2014年国内生产总值(GDP)比2013年增长了12%,由于受到国际贸易的影响,预计2015年比2014年增长7%,若这两年GDP年平均增长率为x%,则x%满足的关系是( )
| A. | 12%+7%=x% | B. | (1+12%)(1+7%)=(1+x%)2 | C. | 12%+7%=2x% | D. | (1+12%)(1+7%)=2(1+x%) |
 已知矩形ABCD中,AB=60cm,BC=40cm,动点P从A点出发,沿着矩形的边自A→B→C→D运动到点D,速度为1cm/s,设运动时间为t(s),△APD的面积为y(cm2).求y与t的解析式.
已知矩形ABCD中,AB=60cm,BC=40cm,动点P从A点出发,沿着矩形的边自A→B→C→D运动到点D,速度为1cm/s,设运动时间为t(s),△APD的面积为y(cm2).求y与t的解析式. 如图,在楼房AB和塔CD之间有一棵树EF,从楼顶A处经过树顶E点恰好看到塔的底部D点,且俯角α为45°.从距离楼底B点1米的P点处经过树顶E点恰好看到塔的顶部C点,且仰角β为30°.已知树高EF=9米,求塔CD的高度.(结果保留根号)
如图,在楼房AB和塔CD之间有一棵树EF,从楼顶A处经过树顶E点恰好看到塔的底部D点,且俯角α为45°.从距离楼底B点1米的P点处经过树顶E点恰好看到塔的顶部C点,且仰角β为30°.已知树高EF=9米,求塔CD的高度.(结果保留根号)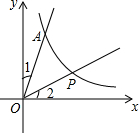 如图,直线y=3x和双曲线y=$\frac{3}{x}$(x>0)交于点A,点P为双曲线上一点,且∠POA=∠1+∠2,求点P的坐标.
如图,直线y=3x和双曲线y=$\frac{3}{x}$(x>0)交于点A,点P为双曲线上一点,且∠POA=∠1+∠2,求点P的坐标.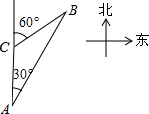 如图,一艘轮船以40海里/时的速度在海面上航行,当它行驶到A处时,发现它的北偏东30°方向有一灯塔B.轮船继续向北航行2小时后到达C处,发现灯塔B在它的北偏东60°方向.此时轮船与灯塔的距离为( )
如图,一艘轮船以40海里/时的速度在海面上航行,当它行驶到A处时,发现它的北偏东30°方向有一灯塔B.轮船继续向北航行2小时后到达C处,发现灯塔B在它的北偏东60°方向.此时轮船与灯塔的距离为( ) 如图,已知AC、BD相交于点O,∠A=∠B,∠1=∠2,AD=BC.试说明△AOD≌△BOC.
如图,已知AC、BD相交于点O,∠A=∠B,∠1=∠2,AD=BC.试说明△AOD≌△BOC.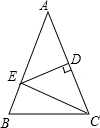 已知△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于点E,D为垂足,连接EC.
已知△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于点E,D为垂足,连接EC.