题目内容
12.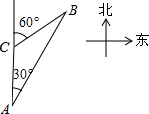 如图,一艘轮船以40海里/时的速度在海面上航行,当它行驶到A处时,发现它的北偏东30°方向有一灯塔B.轮船继续向北航行2小时后到达C处,发现灯塔B在它的北偏东60°方向.此时轮船与灯塔的距离为( )
如图,一艘轮船以40海里/时的速度在海面上航行,当它行驶到A处时,发现它的北偏东30°方向有一灯塔B.轮船继续向北航行2小时后到达C处,发现灯塔B在它的北偏东60°方向.此时轮船与灯塔的距离为( )| A. | 40海里 | B. | 80海里 | C. | 60海里 | D. | 20海里 |
分析 设出CD,先利用锐角三角函数表示出BD,BC,再用三角函数表示出AC,列出方程求出即可.
解答 解:如图,
设CD=x,在Rt△BCD中,∠BCD=60°,
∴BD=$\sqrt{3}$x,BC=2x
在Rt△ABD中,∠A=30°,
∴AD=$\sqrt{3}$BD=$\sqrt{3}$×$\sqrt{3}$x=3x,
∴AC=AD-CD=3x-x=2x,
∵AC=40×2=80,
∴BC=2x=80,
故选B.
点评 此题是解直角三角形题,主要考查了锐角三角函数的定义,解本题的关键是特殊角的三角函数的灵活运用.

练习册系列答案
相关题目
 如图,一次函数y=kx-2的图象与反比例函数的图象交于A、B两点,过A作AC⊥x轴于点C,己知cos∠AOC=$\frac{2\sqrt{5}}{5}$,OA=$\sqrt{5}$
如图,一次函数y=kx-2的图象与反比例函数的图象交于A、B两点,过A作AC⊥x轴于点C,己知cos∠AOC=$\frac{2\sqrt{5}}{5}$,OA=$\sqrt{5}$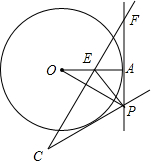 如图,P是⊙O的切线FA上的点,点A为切点,连接OP,OP的垂直平分线FE交OA于点E,连接EP,过点P作PC⊥EP
如图,P是⊙O的切线FA上的点,点A为切点,连接OP,OP的垂直平分线FE交OA于点E,连接EP,过点P作PC⊥EP 如图,在?ABCD中,点E、F分别在边AB、CD上,AE=CF.求证:四边形AECF是平行四边形.
如图,在?ABCD中,点E、F分别在边AB、CD上,AE=CF.求证:四边形AECF是平行四边形.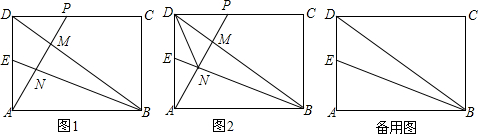
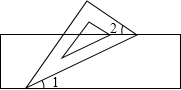 如图,小聪把一块含有60°角的直角三角板的两个顶点放在直尺的对边上,并测得∠1=25°,则∠2的度数是35°.
如图,小聪把一块含有60°角的直角三角板的两个顶点放在直尺的对边上,并测得∠1=25°,则∠2的度数是35°.