题目内容
17. 已知矩形ABCD中,AB=60cm,BC=40cm,动点P从A点出发,沿着矩形的边自A→B→C→D运动到点D,速度为1cm/s,设运动时间为t(s),△APD的面积为y(cm2).求y与t的解析式.
已知矩形ABCD中,AB=60cm,BC=40cm,动点P从A点出发,沿着矩形的边自A→B→C→D运动到点D,速度为1cm/s,设运动时间为t(s),△APD的面积为y(cm2).求y与t的解析式.
分析 分点P在AB、BC、CD上三种情况根据三角形的面积公式列式表示出y与t的函数关系式即可.
解答  解:分三种情况:
解:分三种情况:
①点P在AB上时,AP=tcm,如图1所示:
∴y=$\frac{1}{2}$AD•AP=$\frac{1}{2}$×40t=20t,
即y=20t(0≤t≤60),
②点P在BC上时,如图2所示:
y=$\frac{1}{2}$AD•AB=$\frac{1}{2}$×60×40=1200,
即y=1200(60<t≤100),y是定值;
③点P在CD上时,如图3所示:
AB+BC+CP=tcm,
∴y=$\frac{1}{2}$AD(AB+BC+CD-t)=$\frac{1}{2}$×40(160-t)=3200-20t,
即y=-20t+3200(100<t≤160);
综上所述:y与t的解析式为y=20t(0≤t≤60),或y=1200(60<t≤100),或y=-20t+3200(100<t≤160).
点评 本题考查了矩形的性质、动点问题的函数;根据点P的位置的不同,分三段讨论求解是解题的关键.

练习册系列答案
相关题目
7.若a>b,则下列不等式一定成立的是( )
| A. | -1+a<-1+b | B. | $\frac{a}{2}$<$\frac{b}{2}$ | C. | 2-a>2-b | D. | b-a<0 |
8.下列图形中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
5.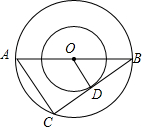 如图,两个圆的圆心都是点O,AB是大圆的直径,大圆的弦BC所在直线与小圆相切于点D.则下列结论不一定成立的是( )
如图,两个圆的圆心都是点O,AB是大圆的直径,大圆的弦BC所在直线与小圆相切于点D.则下列结论不一定成立的是( )
 如图,两个圆的圆心都是点O,AB是大圆的直径,大圆的弦BC所在直线与小圆相切于点D.则下列结论不一定成立的是( )
如图,两个圆的圆心都是点O,AB是大圆的直径,大圆的弦BC所在直线与小圆相切于点D.则下列结论不一定成立的是( )| A. | BD=CD | B. | AC⊥BC | C. | AB=2AC | D. | AC=2OD |
6.在下列现象中,属于平移的是( )
| A. | 小亮荡秋千运动 | B. | 电梯由一楼升到八楼 | ||
| C. | 导弹击中目标后爆炸 | D. | 卫星绕地球运动 |



