题目内容
18．从小到大的不同自然数x1，x2，x3，…x7满足x1+x2+x3+…+x7=2015，则x4+x5+x6+x7的最小值是多少？分析 根据x1，x2，x3，…x7是从小到大的不同自然数可得出x1+x2+x3+…+x7≥x1+x1+1+x1+2+x1+3+x1+4+x1+5+x1+6=7x1+21，求出x1的最大值，进而得出x1+x2+x3的最大值，由此可得出结论．
解答 解：∵x1，x2，x3，…x7是小到大的不同自然数，
∴x1+x2+x3+…+x7≥x1+x1+1+x1+2+x1+3+x1+4+x1+5+x1+6=7x1+21．
∵x1+x2+x3+…+x7=2015，
∴2015≥7x1+21，解得x1≤284$\frac{6}{7}$，
∴x1的最大值是284，
∴284+x2+x3+…+x7=2015≥284+x2+x2+1+x2+2+x2+3+x2+4+x2+5，
∴6x2+15+284≤2015，解得x2≤286，
∴x1的最大值是286；
同理，284+286+x3+…+x7=2015≥284+286+x3+x3+1+x3+2+x3+3+x3+4，解得x3≤287，
∴x3的最大值是287，
∴x1+x2+x3的最大值=284+286+287=857，
∴x4+x5+x6+x7的最小值=2015-857=1158．
点评 本题考查的是有理数的大小比较，根据题意得出x1，x2，x3的最大值是解答此题的关键．
练习册系列答案
相关题目
9．若x＞0，y＜0，则x，x+y，y-x，y中，最小的数是（ ）
| A． | x | B． | x+y | C． | y-x | D． | y |
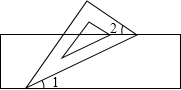如图，小聪把一块含有60°角的直角三角板的两个顶点放在直尺的对边上，并测得∠1=25°，则∠2的度数是35°．
如图，在△ABC中，两条中线BE，CD相交于点O，则OD：OC=$\frac{1}{2}$．
8．
如图所示的立体图形的主视图是（ ）
如图所示的立体图形的主视图是（ ）| A． |  | B． |  | C． |  | D． |  |