题目内容
8.将一组数$\sqrt{2}$,2,$\sqrt{6}$,2$\sqrt{2}$,$\sqrt{10}$,…,2$\sqrt{51}$按图中的方法排列: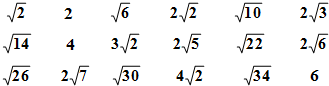
若3$\sqrt{2}$的位置记为(2,3),2$\sqrt{7}$的位置记为(3,2),则这组数中最大有理数的位置记为(17,2).
分析 根据规律发现,被开方数是从2开始的偶数列,最后一个数的被开方数是204,所以最大的有理数是被开方数是196的数,然后求出196在这列数的序号,又6个数一组,求出是第几组第几个数,即可确定它的位置.
解答 解:∵2$\sqrt{51}$=$\sqrt{204}$,
∴这列数中最大的数是$\sqrt{196}$=14,
设196是这列数中的第n个数,则
2n=196,
解得n=98,
观察发现,每6个数一行,即6个数一循环,
∴98÷6=16…2,
∴$\sqrt{196}$是第17组的第2个数.
最大的有理数n的位置记为(17,2).
故答案为:(17,2).
点评 本题利用算术平方根考查了数字的规律变化问题,求出最大的有理数的序号,并6个数作为一个循环组是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.四个命题“①有一个角为60°的等腰三角形中等边三角形;②三角形三边的垂直平分线的交点到三个顶点的距离相等;③三角形的三条角平分线的交点到三边的距离相等;④有两条边对应相等的两个直角三角形全等”中,正确的有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
19.已知 a=2-$\sqrt{5}$,b=$\sqrt{5}$-2,c=5-$\sqrt{5}$,试比较a,b,c的大小是( )
| A. | a<b<c | B. | b<a<c | C. | a<c<b | D. | c<b<a |
16.若a<b,則下列不等式一定成立的是( )
| A. | a2<b2 | B. | ac<bc | C. | ac2<bc2 | D. | a-b<0 |
3.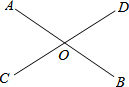 如图,直线AB与直线CD相交于点O,其中∠AOC的对顶角是( )
如图,直线AB与直线CD相交于点O,其中∠AOC的对顶角是( )
 如图,直线AB与直线CD相交于点O,其中∠AOC的对顶角是( )
如图,直线AB与直线CD相交于点O,其中∠AOC的对顶角是( )| A. | ∠A0D | B. | ∠B0D | C. | ∠B0C | D. | ∠A0B |