题目内容
18.已知x-2y+2=0,则$\frac{1}{4}$x2+y2-xy-1的值为0.分析 由已知条件得到x-2y=-2.所求的代数式可以转化为含有(x-2y)形式的代数式,将其整体代入进行求值即可.
解答 解:∵x-2y+2=0,
∴x-2y=-2,
∴$\frac{1}{4}$x2+y2-xy-1,
=$\frac{1}{4}$(x2-4xy+4y2)-1,
=$\frac{1}{4}$(x-2y)2-1,
=$\frac{1}{4}$×(-2)2-1,
=1-1,
=0,
即$\frac{1}{4}$x2+y2-xy-1=0.
故答案是:0.
点评 本题考查了因式分解的应用.用因式分解的方法将式子变形时,根据已知条件,变形的可以是整个代数式,也可以是其中的一部分.

练习册系列答案
相关题目
9.下列计算正确的是( )
| A. | a+a=a2 | B. | a•a2=a2 | C. | (a2)3=a5 | D. | a2(a+1)=a3+a2 |
3.某中学为筹备校庆,准备印制一批纪念册,每册由4张彩页,6张黑白页构成.印制该纪念册的总费用由制版费和印刷费两部分组成,其中制版费的价格为:彩页300元/张,黑白页50元/张;印刷费用与印数的关系见表:
(1)印制这批纪念册需制版费1500元,印制1千册纪念册的印刷费13000元;
(2)若印制这批纪念册共需y元,则:
①当1≤x<5时,求y关于x的函数表达式;
②当y≤60 080元,最多能印多少册?
| 印数x(千册) | 1≤x<5 | x≥5 |
| 彩色(元/张) | 2.2 | 2.0 |
| 黑白(元/张) | 0.7 | 0.6 |
(2)若印制这批纪念册共需y元,则:
①当1≤x<5时,求y关于x的函数表达式;
②当y≤60 080元,最多能印多少册?
10.将四根长度相等的细木条首尾相接,用钉子钉成四边形ABCD,转动这个四边形,使它形状改变.当∠B=90°时(如图甲),测得对角线BD的长为$\sqrt{2}$.当∠B=60°时(如图乙),则对角线BD的长为( )
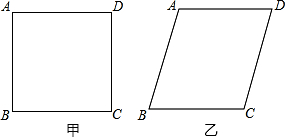

| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
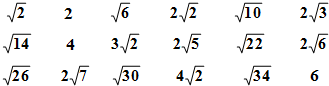
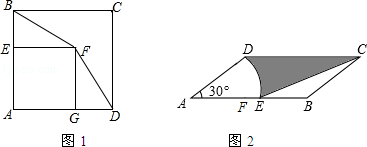
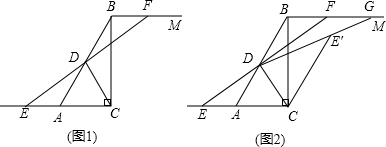
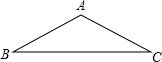 如图,在△ABC中,AB=AC=10,BC=10$\sqrt{3}$.
如图,在△ABC中,AB=AC=10,BC=10$\sqrt{3}$.