题目内容
13.已知方程组$\left\{\begin{array}{l}{x-y=2k}\\{x+3y=1-5k}\end{array}\right.$的解x与y的和为负数,求k的取值范围.分析 利用加减消元法由方程组中的两个方程中得到x,y,再由x、y的和为负数得到关于k的不等式,可求出k的取值范围.
解答 解:方程组$\left\{\begin{array}{l}{x-y=2k}\\{x+3y=1-5k}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{k+1}{4}}\\{y=\frac{1-7k}{4}}\end{array}\right.$,
∵x与y的和为负数,
∴$\frac{k+1}{4}+\frac{1-7k}{4}<0$
解得:k>$\frac{1}{3}$.
点评 本题主要考查二元一次方程组的解,解决本题的关键是求出方程组的解,列出不等式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.某中学为筹备校庆,准备印制一批纪念册,每册由4张彩页,6张黑白页构成.印制该纪念册的总费用由制版费和印刷费两部分组成,其中制版费的价格为:彩页300元/张,黑白页50元/张;印刷费用与印数的关系见表:
(1)印制这批纪念册需制版费1500元,印制1千册纪念册的印刷费13000元;
(2)若印制这批纪念册共需y元,则:
①当1≤x<5时,求y关于x的函数表达式;
②当y≤60 080元,最多能印多少册?
| 印数x(千册) | 1≤x<5 | x≥5 |
| 彩色(元/张) | 2.2 | 2.0 |
| 黑白(元/张) | 0.7 | 0.6 |
(2)若印制这批纪念册共需y元,则:
①当1≤x<5时,求y关于x的函数表达式;
②当y≤60 080元,最多能印多少册?
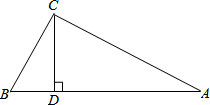 如图所示,已知△ABC中,CD⊥AB于D,AC=4,BC=3,DB=$\frac{9}{5}$.
如图所示,已知△ABC中,CD⊥AB于D,AC=4,BC=3,DB=$\frac{9}{5}$.
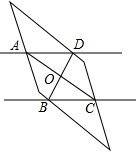 如图,一把宽为$\sqrt{3}$cm的直尺放在一个边长为2$\sqrt{3}$cm,一顶角为30°的菱形纸片上,尺子边缘与菱形纸片相交于点A,B,C,D,连接AC,BD它们相交于点O,则∠AOD的度数为75°.
如图,一把宽为$\sqrt{3}$cm的直尺放在一个边长为2$\sqrt{3}$cm,一顶角为30°的菱形纸片上,尺子边缘与菱形纸片相交于点A,B,C,D,连接AC,BD它们相交于点O,则∠AOD的度数为75°.