题目内容
15.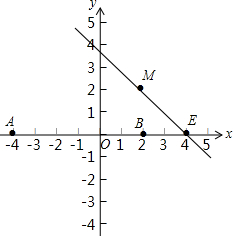 如图,x轴上两个点A(-4,0),B(2,0),直线l经过点E(4,0),M为直线l上的动点,当以A、B、M为顶点所作的直角三角形有且只有三个时,求直线l的解析式.
如图,x轴上两个点A(-4,0),B(2,0),直线l经过点E(4,0),M为直线l上的动点,当以A、B、M为顶点所作的直角三角形有且只有三个时,求直线l的解析式.
分析 本问关键是理解“以A、B、M为顶点所作的直角三角形有且只有三个”的含义.因为过A、B点作x轴的垂线,其与直线l的两个交点均可以与A、B点构成直角三角形,这样已经有符合题意的两个直角三角形;第三个直角三角形从直线与圆的位置关系方面考虑,以AB为直径作圆,当直线与圆相切时,根据圆周角定理,切点与A、B点构成直角三角形.从而问题得解.
解答 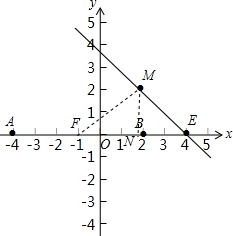 解:以AB为直径作⊙F,圆心为F.过E点作⊙F的切线,这样的切线有2条.
解:以AB为直径作⊙F,圆心为F.过E点作⊙F的切线,这样的切线有2条.
连接FM,过M作MN⊥x轴于点N.
∵A(-4,0),B(2,0),∴F(-1,0),⊙F半径FM=FB=3.
又FE=5,则在Rt△MEF中,
ME=$\sqrt{{5}^{2}-{3}^{2}}$=4,sin∠MFE=$\frac{4}{5}$,cos∠MFE=$\frac{3}{5}$.
在Rt△FMN中,MN=MF•sin∠MFE=3×$\frac{4}{5}$=12$\frac{12}{5}$,
FN=MF•cos∠MFE=3×$\frac{3}{5}$=$\frac{9}{5}$,则ON=$\frac{4}{5}$,
∴M点坐标为($\frac{4}{5}$,$\frac{12}{5}$)
直线l过M($\frac{4}{5}$,$\frac{12}{5}$),E(4,0),
设直线l的解析式为y=kx+b,则有$\left\{\begin{array}{l}{\frac{4}{5}k+b=\frac{12}{5}}\\{4k+b=0}\end{array}\right.$,解得 $\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=3}\end{array}\right.$,
所以直线l的解析式为y=-$\frac{3}{4}$x+3.
同理,可以求得另一条切线的解析式为y=$\frac{3}{4}$x-3.
综上所述,直线l的解析式为y=-$\frac{3}{4}$x+3或y=$\frac{3}{4}$x-3
点评 本题是一次函数的综合题,考查了切线的性质,勾股定理的应用,待定系数法求一次函数的解析式等,理解“以A、B、M为顶点所作的直角三角形有且只有三个”的含义是解题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | 0 | B. | 2 | C. | 3 | D. | 4 |
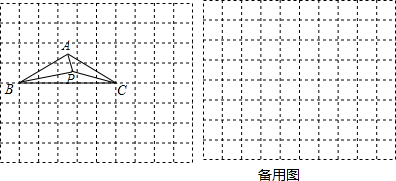
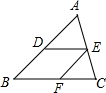 如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,若DE∥BC,EF∥AB,则下面所列比例式中正确的是( )
如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,若DE∥BC,EF∥AB,则下面所列比例式中正确的是( )| A. | $\frac{AD}{BD}$=$\frac{DE}{BC}$ | B. | $\frac{BF}{BC}$=$\frac{EF}{AD}$ | C. | $\frac{AE}{EC}$=$\frac{BF}{CF}$ | D. | $\frac{EF}{AB}$=$\frac{DE}{BC}$ |
 如图是某校“最喜爱的球类运动”统计图(每名学生分别选了一项球类运动),已知选羽毛球的人数比选乒乓球的人数少8人,则该校选篮球的学生人数为16名.
如图是某校“最喜爱的球类运动”统计图(每名学生分别选了一项球类运动),已知选羽毛球的人数比选乒乓球的人数少8人,则该校选篮球的学生人数为16名.