题目内容
12.列出下列问题中的关系式,并指出变量与常量.(1)一支蜡烛长20cm,每分钟燃烧的长度为0.1cm,燃烧t分钟后剩下的长度为l;
(2)用16cm长的绳子围成长方形,设长方形的长为xcm,面积为Scm2;
(3)如果一盒圆珠笔12支,售价为18元,那么购买x支圆珠笔应付款y元.
分析 (1)根据:剩余长度=蜡烛总长-燃烧掉的长度,列函数关系式;
(2)根据:面积=长×宽,列函数关系式;
(3)根据:应付款=圆珠笔单件×圆珠笔数量,列函数关系式.
解答 解:(1)l=20-0.1t,常量是20,0.1,变量是t,l;
(2)S=x•$\frac{16-2x}{2}$=-x2+8x,常量是8,变量是x,S;
(3)y=$\frac{18}{12}•x$=1.5x,常量是1.5,变量是x,y.
点评 本题考查了函数关系式:根据实际问题的数量关系用解析式法表示实际问题中两变化的量之间的关系,常量和变量的定义,常量就是在变化过程中不变的量,变量就是可以取到不同数值的量.

练习册系列答案
相关题目
3.点O是矩形ABCD内任意一点,点O到点A、B、C的距离分别为a、b、c,那么点O到点D的距离为( )
| A. | $\sqrt{{a}^{2}+{b}^{2}+{c}^{2}}$ | B. | $\sqrt{{a}^{2}-{b}^{2}-{c}^{2}}$ | C. | $\sqrt{{a}^{2}-{b}^{2}+{c}^{2}}$ | D. | $\sqrt{-{c}^{2}+{b}^{2}+{a}^{2}}$ |
17.已知单项式-xm-2y3与$\frac{2}{3}$xny2m-3n是同类项,那么m,n的值分别是( )
| A. | $\left\{\begin{array}{l}{m=3}\\{n=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{m=3}\\{n=1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{m=-3}\\{n=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{m=-3}\\{n=-1}\end{array}\right.$ |
2.已知△ABC∽△A′B′C′,sinA=m,sinA′=n,则m和n的大小关系为( )
| A. | m<n | B. | m>n | C. | m=n | D. | 无法确定 |
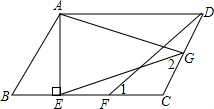 已知,如图,在?ABCD中,AE⊥BC,垂足为E,CE=CD,F为CE的中点,G为CD上的一点,连接DF,EG,AG,∠1=∠2.
已知,如图,在?ABCD中,AE⊥BC,垂足为E,CE=CD,F为CE的中点,G为CD上的一点,连接DF,EG,AG,∠1=∠2.