题目内容
 如图,一次函数y=kx+b的图象与坐标轴分别交于A、B两点,与反比例函数y=
如图,一次函数y=kx+b的图象与坐标轴分别交于A、B两点,与反比例函数y=| m |
| x |
(1)求一次函数与反比例函数的解析式;
(2)直接写出当x<0时,kx+b-
| m |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)根据三角形面积求出OA,得出A、B的坐标,代入一次函数的解析式即可求出解析式,把x=8代入求出D的坐标,把D的坐标代入反比例函数的解析式求出即可;
(2)求出两函数的另一个交点,即可得出答案.
(2)求出两函数的另一个交点,即可得出答案.
解答:解:(1)∵S△AOB=4,OB=4
∴OA=2,
∴B(4,0),A(0,-2),
代入y=kx+b得:
,
解得:k=
,b=-2,
∴一次函数y=
x-2,
∵OD=8,
∴D(8,0),当x=8时,y=
×8-2=2
∴C(8,2),
∴反比例函数的解析式是y=
;
(2)解方程组
得两图象的另一个交点坐标为(-4,-4),
∴
x-2>
,且x<0,
∴-4<x<0,
即当x<0时,kx+b-
>0的解集是-4<x<0.
∴OA=2,
∴B(4,0),A(0,-2),
代入y=kx+b得:
|
解得:k=
| 1 |
| 2 |
∴一次函数y=
| 1 |
| 2 |
∵OD=8,
∴D(8,0),当x=8时,y=
| 1 |
| 2 |
∴C(8,2),
∴反比例函数的解析式是y=
| 16 |
| x |
(2)解方程组
|
∴
| 1 |
| 2 |
| 16 |
| x |
∴-4<x<0,
即当x<0时,kx+b-
| m |
| x |
点评:本题考查了用待定系数法求出函数的解析式,一次函数和和反比例函数的交点问题,函数的图象的应用,主要考查学生的观察图形的能力和计算能力.

练习册系列答案
相关题目
 如图,A、B、C三点在⊙O上,且∠ABO=50°,则∠ACB等于( )
如图,A、B、C三点在⊙O上,且∠ABO=50°,则∠ACB等于( )| A、100° | B、80° |
| C、50° | D、40° |
下列说法正确的是( )
| A、三角形的内心是这个三角形三条边中垂线的交点 |
| B、矩形的对角线相等的逆命题是真命题 |
| C、一组数据2、9、7、5、4、8、5、3的中位数是5 |
| D、正六边形的外角和是720度 |
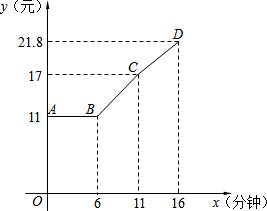 某市出租车按里程计费标准为:不超过3公里部分,计费11元,超过3公里部分,按每公里2.4元计费.现在在此基础上,如果车速不超过12公里/小时,那么再加收0.48元/分钟,这项费用叫做“双计费”.图中三段折线表示某时间段内,一辆出租车的计费总额y(元)与行驶时间x(分钟)的函数关系(出租车在每段上均匀速行驶).
某市出租车按里程计费标准为:不超过3公里部分,计费11元,超过3公里部分,按每公里2.4元计费.现在在此基础上,如果车速不超过12公里/小时,那么再加收0.48元/分钟,这项费用叫做“双计费”.图中三段折线表示某时间段内,一辆出租车的计费总额y(元)与行驶时间x(分钟)的函数关系(出租车在每段上均匀速行驶). 已知抛物线y=ax2-2ax-4与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,△ABC的面积为12.
已知抛物线y=ax2-2ax-4与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,△ABC的面积为12. 如图,在平面直角坐标系中,直线l是第二、四象限的角平分线.
如图,在平面直角坐标系中,直线l是第二、四象限的角平分线.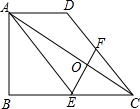 已知:如图,在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,点E是BC的中点、F是CD上的点,联结AE、EF、AC.
已知:如图,在梯形ABCD中,AD∥BC,∠ABC=90°,BC=2AD,点E是BC的中点、F是CD上的点,联结AE、EF、AC.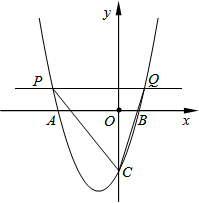 如图,在平面直角坐标系xOy中,二次函数y=ax2+bx-3(a,b是常数)的图象与x轴交于点A(-3,0)和点B(1,0),与y轴交于点C.动直线y=t(t为常数)与抛物线交于不同的两点P、Q.
如图,在平面直角坐标系xOy中,二次函数y=ax2+bx-3(a,b是常数)的图象与x轴交于点A(-3,0)和点B(1,0),与y轴交于点C.动直线y=t(t为常数)与抛物线交于不同的两点P、Q.