题目内容
5.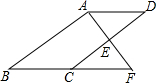 如图,E是?ABCD的边CD的中点,延长AE交BC的延长线于点F.
如图,E是?ABCD的边CD的中点,延长AE交BC的延长线于点F.(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.
分析 (1)由平行四边形的性质得出AD∥BC,AB∥CD,证出∠DAE=∠F,∠D=∠ECF,由AAS证明△ADE≌△FCE即可;
(2)由全等三角形的性质得出AE=EF=3,由平行线的性质证出∠AED=∠BAF=90°,由勾股定理求出DE,即可得出CD的长.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠DAE=∠F,∠D=∠ECF,
∵E是?ABCD的边CD的中点,
∴DE=CE,
在△ADE和△FCE中,
$\left\{\begin{array}{l}{∠DAE=∠F}&{\;}\\{∠D=∠ECF}&{\;}\\{DE=CE}&{\;}\end{array}\right.$,
∴△ADE≌△FCE(AAS);
(2)解:∵△ADE≌△FCE,
∴AE=EF=3,
∵AB∥CD,
∴∠AED=∠BAF=90°,
在?ABCD中,AD=BC=5,
∴DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴CD=2DE=8.
点评 此题考查了平行四边形的性质、全等三角形的判定方法、勾股定理;熟练掌握平行四边形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
15.已知抛物线y=ax2+bx+c(b>a>0)与x轴最多有一个交点,现有以下四个结论:
①该抛物线的对称轴在y轴左侧;
②关于x的方程ax2+bx+c+2=0无实数根;
③a-b+c≥0;
④$\frac{a+b+c}{b-a}$的最小值为3.
其中,正确结论的个数为( )
①该抛物线的对称轴在y轴左侧;
②关于x的方程ax2+bx+c+2=0无实数根;
③a-b+c≥0;
④$\frac{a+b+c}{b-a}$的最小值为3.
其中,正确结论的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
13.已知甲煤场有煤518吨,乙煤场有煤106吨,为了使甲煤场存煤是乙煤场的2倍,需要从甲煤场运煤到乙煤场,设从甲煤场运煤x吨到乙煤场,则可列方程为( )
| A. | 518=2(106+x) | B. | 518-x=2×106 | C. | 518-x=2(106+x) | D. | 518+x=2(106-x) |
20.六边形的内角和是( )
| A. | 540° | B. | 720° | C. | 900° | D. | 1080° |
14.下列运算结果正确的是( )
| A. | a2+a3=a5 | B. | (a2)3=a6 | C. | a2•a3=a6 | D. | 3a-2a=1 |
10.若等腰三角形的一个内角等于92°,则另两个角的度数分别是( )
| A. | 92°、16° | B. | 44°、44° | ||
| C. | 92°、16°或44°、44° | D. | 46°、46° |

 如图,四边形ABCD内接于⊙O,AB是直径,过C点的切线与AB的延长线交于P点,若∠P=40°,则∠D的度数为115°.
如图,四边形ABCD内接于⊙O,AB是直径,过C点的切线与AB的延长线交于P点,若∠P=40°,则∠D的度数为115°.