题目内容
14.如果x=y,a为有理数,那么下列等式不一定成立的是( )| A. | 1-y=1-x | B. | x2=y2 | C. | $\frac{x}{a}$=$\frac{y}{a}$ | D. | ax=ay |
分析 A、等式两边先同时乘-1,然后再同时加1即可;
B、根据乘方的定义可判断;
C、根据等式的性质2判断即可;
D、根据等式的性质2判断即可.
解答 解:A、∵x=y,
∴-x=-y.
∴-x+1=-y+1,即1-y=1-x,故A一定成立,与要求不符;
B、如果x=y,则x2=y2,故B一定成立,与要求不符;
C、当a=0时,$\frac{x}{a}=\frac{y}{a}$无意义,故C不一定成立,与要求相符;
D、由等式的性质可知:ax=ay,故D一定成立,与要求不符.
故选:C.
点评 本题主要考查的是等式的性质,掌握等式的性质是解题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
5. 如图所示,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则DF:FC=( )
如图所示,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则DF:FC=( )
 如图所示,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则DF:FC=( )
如图所示,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则DF:FC=( )| A. | 1:3 | B. | 1:4 | C. | 2:3 | D. | 1:2 |
2.一等腰三角形底边长为8cm,腰长为5cm,则腰上的高为( )
| A. | 3cm | B. | $\frac{5}{4}$cm | C. | $\frac{24}{5}$cm | D. | $\frac{12}{5}$cm |
9.-$\frac{1}{6}$的相反数是( )
| A. | -6 | B. | -$\frac{1}{6}$ | C. | $\frac{1}{6}$ | D. | 6 |
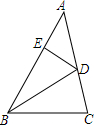 如图,BD是△ABC的角平分线,DE⊥AB,垂足为E,△ABC的面积为70,AB=16,BC=12,则DE的长为5.
如图,BD是△ABC的角平分线,DE⊥AB,垂足为E,△ABC的面积为70,AB=16,BC=12,则DE的长为5.