题目内容
15.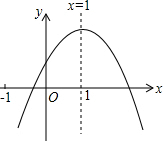 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①abc>0;②a-b+c<0;③当x<0时,y<0;④9a2+3b+c<0;⑤2a-b-1<0.
其中错误的结论的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①根据图象的开口方向,可得a的范围,根据对称轴,可得b的范围,根据图象与y轴的交点,可得c的范围,根据有理数的乘法,可得答案;
②根据自变量为-1时函数值,可得答案;
③根据观察函数图象的纵坐标,可得答案;
④根据对称性,可得自变量为3时的函数值,可得答案;
⑤根据对称轴,可得b与a的关系,根据a的取值范围,可得答案.
解答 解:①图象开口向下,得a<0,
对称轴x=-$\frac{b}{2a}$=1>0,得b=-2a>0,
图象与y轴的交点在x轴的上方,得c>0abc<,故①错误;
②由图象,得x=-1时,y<0,即a-b+c<0,故②正确;
③由图象,得
图象与y轴的交点在x轴的上方,即当x<0时,y有大于零的部分,故③错误;
④由对称性,得
x=3与x=-1关于x=1对称.
由x=-1时,y<0,得
x=3时,y=9a+3b+c<0,
故④正确;
⑤由图象的开口方向,得a<0,
由对称轴,得x=-$\frac{b}{2a}$=1,解得b=-2a,
2a-b-1=2a-(-2a)-1=4a-1<-1,
故⑤正确.
故选:B.
点评 本题考查了二次函数图象与系数的关系,根据开口判断a的符号,根据与x轴,y轴的交点判断c的值以及b用a表示出的代数式.难点是推断出当x=3时,应有y<0.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
3.化简:$\sqrt{\frac{{x}^{2}y}{x}}$•$\sqrt{xy}$=( )
| A. | xy | B. | y | C. | x | D. | x$\sqrt{y}$ |
20.下列代数式中,符合书写规则的是( )
| A. | $1{\frac{1}{2}^{\;}}$x | B. | x÷y | C. | m×2 | D. | 3mn |
 粗心的小马在画数轴时只标注了单位长度(一格表示1个单位长度)和正方向,而忘记了标注原点(如图所示),若点B和点C表示的两个数的绝对值相等,则点A表示的数为-4,点B表示的数为-3,点C表示的数为3.
粗心的小马在画数轴时只标注了单位长度(一格表示1个单位长度)和正方向,而忘记了标注原点(如图所示),若点B和点C表示的两个数的绝对值相等,则点A表示的数为-4,点B表示的数为-3,点C表示的数为3.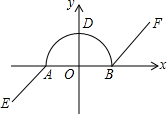 如图,在平面直角坐标系中,我们把由两条射线AE、BF和以AB为直径的半圆的组成的图形叫做π图形(注:不含线段AB),已知A(-1,0),B(1,0),AE∥BF,且半圆与y轴的交点D在射线AE的反向延长线上.
如图,在平面直角坐标系中,我们把由两条射线AE、BF和以AB为直径的半圆的组成的图形叫做π图形(注:不含线段AB),已知A(-1,0),B(1,0),AE∥BF,且半圆与y轴的交点D在射线AE的反向延长线上.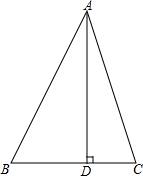 如图,△ABC中,∠A=45°,过点A作AD⊥BC,BD=2,BC=3,求S△ABC.
如图,△ABC中,∠A=45°,过点A作AD⊥BC,BD=2,BC=3,求S△ABC.