题目内容
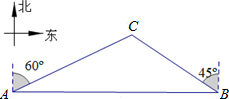 如图,一天,我国一渔政船航行到A处时,发现正东方向的我领海区域B处有一可疑渔船,正在以12海里/小时的速度向西北方向航行,我渔政船立即沿北偏东60°方向航行,1.5小时后,在我领海区域的C处截获可疑渔船,问我渔政船的航行路程是多少海里?(结果精确到0.1海里,
如图,一天,我国一渔政船航行到A处时,发现正东方向的我领海区域B处有一可疑渔船,正在以12海里/小时的速度向西北方向航行,我渔政船立即沿北偏东60°方向航行,1.5小时后,在我领海区域的C处截获可疑渔船,问我渔政船的航行路程是多少海里?(结果精确到0.1海里,| 2 |
考点:解直角三角形的应用-方向角问题
专题:
分析:作CD⊥AB于点D,垂足为D,首先在Rt△BCD中求得CD的长,然后在Rt△ACD中求得AC的长即可.
解答:解:作CD⊥AB于点D,垂足为D,
在Rt△BCD中,
∵BC=12×1.5=18(海里),∠CBD=45°,
∴CD=BC•sin45°=18×
=9
(海里),
则在Rt△ACD中,
AC=
=9
×2=18
≈25.5(海里).
故我渔政船航行了约25.5海里.

在Rt△BCD中,
∵BC=12×1.5=18(海里),∠CBD=45°,
∴CD=BC•sin45°=18×
| ||
| 2 |
| 2 |
则在Rt△ACD中,
AC=
| CD |
| sin30° |
| 2 |
| 2 |
故我渔政船航行了约25.5海里.
点评:本题考查了解直角三角形的应用,解题的关键是从实际问题中构造出直角三角形并利用三角函数的知识求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
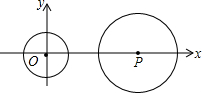 如图,平面直角坐标系中,⊙O半径长为1,点P(a,0),⊙P的半径长为2,把⊙P向左平移,与⊙P与⊙O相切时,a的值为( )
如图,平面直角坐标系中,⊙O半径长为1,点P(a,0),⊙P的半径长为2,把⊙P向左平移,与⊙P与⊙O相切时,a的值为( )| A、3 | B、1 | C、1,3 | D、±1,3 |
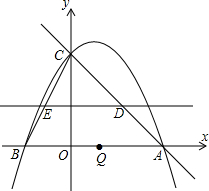 如图,抛物线y=ax2+bx+c交x轴于A(4,0),B(-2,0)两点,交y轴于点C(0,4).
如图,抛物线y=ax2+bx+c交x轴于A(4,0),B(-2,0)两点,交y轴于点C(0,4). 如图,在菱形ABCD中,AB=BD,点E、F分别在AB、AD上,且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论:
如图,在菱形ABCD中,AB=BD,点E、F分别在AB、AD上,且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论: