题目内容
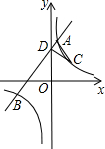 如图,已知直线y=mx+b与双曲线y=
如图,已知直线y=mx+b与双曲线y=| k |
| x |
(1)请写出直线y=mx+b与双曲线y=
| k |
| x |
(2)根据图象回答:当x取何值时,反比例函数的值大于一次函数的值.
(3)若双曲线y=
| k |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)已知直线y=mx+b与双曲线y=
交于B(-4,-2),代入即可k的值,从而求得双曲线的解析式y=
,把A(n,8)代入y=
,求得n的值,所以A(1,8),把A、B分别代入直线y=mx+b中即可求得直线的解析式.(2)反比例函数图象在直线的上方反比例函数的值大于一次函数的值.(3)延长CA交y轴于P,三角形PDC的面积减去三角形PDA的面积即可求得.
| k |
| x |
| 8 |
| x |
| 8 |
| x |
解答:解:(1)∵双曲线y=
经过B(-4,-2),
∴-2=
,
解得k=8;
∴双曲线y=
的表达式为y=
.
∵双曲线y=
经过A(n,8),
∴8=
,
解得n=1.
∴A(1,8).
∵直线y=mx+b与双曲线y=
交于A(1,8),B(-4,-2)两点;
∴
解得
;
∴直线y=mx+b的表达式为y=2x+6.
(2)∵A(1,8)、B(-4,-2),
∴当0<x<1或x<-4时反比例函数的值大于一次函数的值.
(3)延长CA交y轴于P,
∵C的纵坐标为4,
代入y=
.
得x=2,
∴C(2,4),
∵A(1,8),设直线AC的解析式y=kx+b;
解得k=-4,b=12,
∴P(0,12),
∴DP=6,
∴S△ADC=S△PDC-S△PAD=
×6×2-
×6×1=3.

| k |
| x |
∴-2=
| k |
| -4 |
解得k=8;
∴双曲线y=
| k |
| x |
| 8 |
| x |
∵双曲线y=
| k |
| x |
∴8=
| 8 |
| n |
解得n=1.
∴A(1,8).
∵直线y=mx+b与双曲线y=
| k |
| x |
∴
|
解得
|
∴直线y=mx+b的表达式为y=2x+6.
(2)∵A(1,8)、B(-4,-2),
∴当0<x<1或x<-4时反比例函数的值大于一次函数的值.
(3)延长CA交y轴于P,
∵C的纵坐标为4,
代入y=
| 8 |
| x |
得x=2,
∴C(2,4),
∵A(1,8),设直线AC的解析式y=kx+b;
|
解得k=-4,b=12,
∴P(0,12),
∴DP=6,
∴S△ADC=S△PDC-S△PAD=
| 1 |
| 2 |
| 1 |
| 2 |

点评:本题考查了一次函数与反比例函数的交点问题,用待定系数法求函数的解析式的应用,以及通过图象能够直观的看出函数值的大小,利用交点求三角形面积的方法,主要考查学生的计算能力.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
下列计算正确的是( )
| A、x•x2=x2 |
| B、(xy)2=xy2 |
| C、x2+x2=x4 |
| D、(x2)3=x6 |

 如图,兰兰站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,测得小船C的俯角是∠FDC=30°,若兰兰的眼睛与地面的距离是1.5米,BG=1米,BG平行于AC所在的直线,迎水坡的坡度i=4:3,坡高BE=8米,求小船C到岸边的距离CA的长?(参考数据:
如图,兰兰站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,测得小船C的俯角是∠FDC=30°,若兰兰的眼睛与地面的距离是1.5米,BG=1米,BG平行于AC所在的直线,迎水坡的坡度i=4:3,坡高BE=8米,求小船C到岸边的距离CA的长?(参考数据: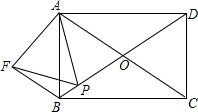 如图,矩形ABCD的对角线AC、BD交于点O,且∠AOB=60°,点P为线段BO上任意一点,以AP为边作等边三角形APF.连结BF,求证:BF=OP.
如图,矩形ABCD的对角线AC、BD交于点O,且∠AOB=60°,点P为线段BO上任意一点,以AP为边作等边三角形APF.连结BF,求证:BF=OP.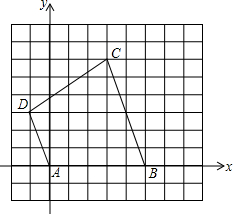 如图,在10×10的正方形网格纸中,A(0,0),B(5,0),C(3,6),D(-1,3),依次连接A、B、C、D四点得到四边形ABCD.
如图,在10×10的正方形网格纸中,A(0,0),B(5,0),C(3,6),D(-1,3),依次连接A、B、C、D四点得到四边形ABCD. 如图,点O在边长为8的正方形ABCD的AD边上运动(4<C)A<8),以O为圆心,OA长为半径作圆,交CD于点E,连接OE、AE,过点E作直线EF交BC于点F,且∠CEF=2∠DAE.
如图,点O在边长为8的正方形ABCD的AD边上运动(4<C)A<8),以O为圆心,OA长为半径作圆,交CD于点E,连接OE、AE,过点E作直线EF交BC于点F,且∠CEF=2∠DAE.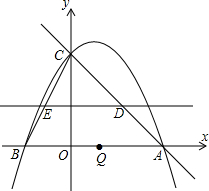 如图,抛物线y=ax2+bx+c交x轴于A(4,0),B(-2,0)两点,交y轴于点C(0,4).
如图,抛物线y=ax2+bx+c交x轴于A(4,0),B(-2,0)两点,交y轴于点C(0,4). 如图,在菱形ABCD中,AB=BD,点E、F分别在AB、AD上,且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论:
如图,在菱形ABCD中,AB=BD,点E、F分别在AB、AD上,且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论: