题目内容
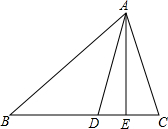 如图所示,在△ABC中,∠B=30°,∠C=80°,AD是△ABC的角平分线,AE是△ABC的高.①求∠DAE的度数;②求∠ADB的度数.
如图所示,在△ABC中,∠B=30°,∠C=80°,AD是△ABC的角平分线,AE是△ABC的高.①求∠DAE的度数;②求∠ADB的度数.考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)由三角形的内角和定理,求出∠BAC的度数,再根据角平分线的定义求出∠BAD的度数,再根据AE是△ABC的高和三角形的内角和定理得出∠BAE的度数,即可得出∠DAE;
(2)利用三角形的外角的性质得出∠ADB的度数即可.
(2)利用三角形的外角的性质得出∠ADB的度数即可.
解答:解:(1)在△ABC中,
∵∠BAC=180°-∠B-∠C=70°,
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD=35°.
又∵AE是BC边上的高,
∴∠AEB=90°,
∵在△ABE中∠BAE=90°-∠B=60°,
∴∠DAE=∠BAE-∠BAD=25°,
(2)∠ADB=∠CAD+∠C=115°.
∵∠BAC=180°-∠B-∠C=70°,
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD=35°.
又∵AE是BC边上的高,
∴∠AEB=90°,
∵在△ABE中∠BAE=90°-∠B=60°,
∴∠DAE=∠BAE-∠BAD=25°,
(2)∠ADB=∠CAD+∠C=115°.
点评:本题考查三角形的内角和定理及角平分线的性质,高线的性质,三角形外角的性质,解答的关键是三角形的内角和定理,一定要熟练于心,难度适中.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
小亮在解不等式组
时,解法步骤如下:
解不等式①,得x>3,…第一步;
解不等式②,得x>-8,…第二步;
所有原不等式组组的解集为-8<x<3…第三步.
对于以上解答,你认为下列判断正确的是( )
|
解不等式①,得x>3,…第一步;
解不等式②,得x>-8,…第二步;
所有原不等式组组的解集为-8<x<3…第三步.
对于以上解答,你认为下列判断正确的是( )
| A、解答有误,错在第一步 |
| B、解答有误,错在第二步 |
| C、解答有误,错在第三步 |
| D、原解答正确无误 |
 两个一次函数的图象如图,
两个一次函数的图象如图, 如图,CE平分∠BCD,∠1=∠2=70°,∠3=40°,AB和CD是否平行?请说明理由.
如图,CE平分∠BCD,∠1=∠2=70°,∠3=40°,AB和CD是否平行?请说明理由.
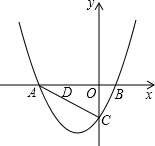 已知二次函数y=
已知二次函数y=