题目内容
长沙市某商业公司生产的某种时令商品每件成本为20元,经过市场调研发现,这种商品在未来40天内的日销售量 m(件)与时间t(天)的关系如下表:
未来40天内,该商品每天的价格y(元∕件)与时间t(天)的函数关系式为:
y=
根据以上提供的条件解决下列问题:
(1)认真分析上表中的数据,用所学过的一次函数的知识分别确定1≤t≤20,21≤t≤40时,满足这些数据的m(件)与t(天)之间的关系式;
(2)请预测未来40天中哪一天的日销售利润最大,最大的销售利润是多少?
(3)在实际销售的前20天中,该公司决定每销售一件商品就捐赠a元利润(a<4)给希望工程.公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润随时间t(天)的增大而增大,求a的最小值.
| 时间t(天) | 1 | 3 | 10 | 20 | 21 | 22 | 40 |
| 日销售量 m(件) | 98 | 94 | 80 | 60 | 61 | 62 | 80 |
y=
|
根据以上提供的条件解决下列问题:
(1)认真分析上表中的数据,用所学过的一次函数的知识分别确定1≤t≤20,21≤t≤40时,满足这些数据的m(件)与t(天)之间的关系式;
(2)请预测未来40天中哪一天的日销售利润最大,最大的销售利润是多少?
(3)在实际销售的前20天中,该公司决定每销售一件商品就捐赠a元利润(a<4)给希望工程.公司通过销售记录发现,前20天中,每天扣除捐赠后的日销售利润随时间t(天)的增大而增大,求a的最小值.
考点:二次函数的应用
专题:
分析:(1)分别利用待定系数法求一次函数解析式解答即可;
(2)根据t的取值范围分两段根据利润=单件的利润×销售量,再根据二次函数的最值问题解答;
(3)整理得到捐赠后的利润表达式,再根据二次函数的增减性从对称轴考虑列出不等式,然后求解即可.
(2)根据t的取值范围分两段根据利润=单件的利润×销售量,再根据二次函数的最值问题解答;
(3)整理得到捐赠后的利润表达式,再根据二次函数的增减性从对称轴考虑列出不等式,然后求解即可.
解答:解:(1)当1≤t≤20(t为整数)时,将
和
代入一次函数m=kt+b中,有
,
解得
,
所以m=-2t+100;
当21≤t≤40(t为整数)时,将
和
代入一次函数m=kt+b中,有
,
解得
,
所以m=t+40,
综上可得:m=
;
(2)设前20天日销售利润为P1元,后20天的日销售利润为P2元,
当1≤t≤20(t为整数)时,P1=(-2t+100)(
t+25-20)=-
t2+15t+500,
=-
(t-15)2+612.5,
所以,t=15时,P1有最大值612.5元;
当21≤t≤40(t为整数)时,P2=(t+40)(-
t+40-20),
=-
t2+800,
所以,t=21时,P2有最大值-
×212+800=579.5元,
综上可得:当t=15时,利润最大,为612.5元;
(3)当1≤t≤20(t为整数)时,
P1=(-2t+100)(
t+25-20-a)=-
t2+(15+2a)t+500-100a,
对称轴为:t=
=15+2a,
∵前20天中,每天扣除捐赠后的日销售利润随时间t(天)的增大而增大,
∴15+2a≥20,
解得a≥2.5,
所以,a的最小值是2.5.
|
|
|
解得
|
所以m=-2t+100;
当21≤t≤40(t为整数)时,将
|
|
|
解得
|
所以m=t+40,
综上可得:m=
|
(2)设前20天日销售利润为P1元,后20天的日销售利润为P2元,
当1≤t≤20(t为整数)时,P1=(-2t+100)(
| 1 |
| 4 |
| 1 |
| 2 |
=-
| 1 |
| 2 |
所以,t=15时,P1有最大值612.5元;
当21≤t≤40(t为整数)时,P2=(t+40)(-
| 1 |
| 2 |
=-
| 1 |
| 2 |
所以,t=21时,P2有最大值-
| 1 |
| 2 |
综上可得:当t=15时,利润最大,为612.5元;
(3)当1≤t≤20(t为整数)时,
P1=(-2t+100)(
| 1 |
| 4 |
| 1 |
| 2 |
对称轴为:t=
| -(15+2a) | ||
2×(-
|
∵前20天中,每天扣除捐赠后的日销售利润随时间t(天)的增大而增大,
∴15+2a≥20,
解得a≥2.5,
所以,a的最小值是2.5.
点评:本题考查了二次函数的应用,主要利用了待定系数法求一次函数解析式,利用二次函数的增减性求二次函数的最值问题,理清题目数量关系列出利润表达式是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
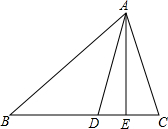 如图所示,在△ABC中,∠B=30°,∠C=80°,AD是△ABC的角平分线,AE是△ABC的高.①求∠DAE的度数;②求∠ADB的度数.
如图所示,在△ABC中,∠B=30°,∠C=80°,AD是△ABC的角平分线,AE是△ABC的高.①求∠DAE的度数;②求∠ADB的度数. 如图,小刀的刀片上、下是平行的,刀柄外形是一个含直角的梯形下底挖去一小半圆(见图中标示),则∠1+∠2的度数为
如图,小刀的刀片上、下是平行的,刀柄外形是一个含直角的梯形下底挖去一小半圆(见图中标示),则∠1+∠2的度数为