题目内容
 如图,CE平分∠BCD,∠1=∠2=70°,∠3=40°,AB和CD是否平行?请说明理由.
如图,CE平分∠BCD,∠1=∠2=70°,∠3=40°,AB和CD是否平行?请说明理由.考点:平行线的判定
专题:
分析:先由角平分线的定义得出∠4=∠1=70°,∠BCD=2∠1=140°,等量代换得到∠4=∠2=70°,根据内错角相等,两直线平行得出AD∥BC,再由两直线平行,同位角相等得出∠B=∠3=40°,则∠B+∠BCD=40°+140°=180°,根据同旁内角互补,两直线平行证明AB∥CD.
解答:解:AB和CD平行.理由如下:
∵CE平分∠BCD,
∴∠4=∠1=70°,∠BCD=2∠1=140°,
∵∠1=∠2=70°,
∴∠4=∠2=70°,
∴AD∥BC,
∴∠B=∠3=40°,
∴∠B+∠BCD=40°+140°=180°,
∴AB∥CD.
∵CE平分∠BCD,
∴∠4=∠1=70°,∠BCD=2∠1=140°,
∵∠1=∠2=70°,
∴∠4=∠2=70°,
∴AD∥BC,
∴∠B=∠3=40°,
∴∠B+∠BCD=40°+140°=180°,
∴AB∥CD.
点评:本题主要考查了平行线的判定与性质,用到的知识点:内错角相等,两直线平行;同旁内角互补,两直线平行;两直线平行,同位角相等.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
方程
x2-
x+
=0的根的情况是( )
| 1 |
| 2 |
| 5 |
| 5 |
| A、有两个相等的实数根 |
| B、有两个不相等的实数根 |
| C、有一个实数根 |
| D、没有实数根 |


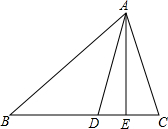 如图所示,在△ABC中,∠B=30°,∠C=80°,AD是△ABC的角平分线,AE是△ABC的高.①求∠DAE的度数;②求∠ADB的度数.
如图所示,在△ABC中,∠B=30°,∠C=80°,AD是△ABC的角平分线,AE是△ABC的高.①求∠DAE的度数;②求∠ADB的度数.