题目内容
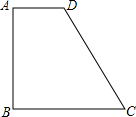如图，在直角梯形ABCD中，AD∥BC，AB⊥BC，AD=2，AB=3，BC=4，则CD的长是考点：直角梯形
专题：
分析：利用直角梯形的性质结合勾股定理得出DC的长．
解答：
解：过点D作DE⊥BC于点E，
∵AD∥BC，AB⊥BC，AD=2，AB=3，BC=4，
∴AD=BE=2，DE=AB=3，则EC=2，
∴DC=
=
=
．
故答案为：
．
解：过点D作DE⊥BC于点E，∵AD∥BC，AB⊥BC，AD=2，AB=3，BC=4，
∴AD=BE=2，DE=AB=3，则EC=2，
∴DC=
| DE2+EC2 |
| 32+22 |
| 13 |
故答案为：
| 13 |
点评：此题主要考查了直角梯形以及勾股定理等知识，正确利用勾股定理得出是解题关键．
练习册系列答案
相关题目
如图，在平行四边形ABCD中AC，BD相交于点O，E，F分别是OB、OD的中点．
在△ABC中，边BC的长与BC边上的高线长之和为20．
观察下面图形，并回答问题．