题目内容
在Rt△ABC中，∠C=90°，sinA=
，BC=20，则△ABC的面积为 ．
| 4 |
| 5 |
考点：解直角三角形
专题：
分析：根据正弦函数的定义即可求得AB的长，然后根据勾股定理即可求得AC的长，则三角形的面积可以求得．
解答：解：∵在Rt△ABC中，∠C=90°，sinA=
=
，
∴AB=
=20÷
=25，
∴AC=
=
=15，
则△ABC的面积为：
AC•BC=
×15×20=150．
故答案为：150．
| BC |
| AB |
| 4 |
| 5 |
∴AB=
| BC |
| sinA |
| 4 |
| 5 |
∴AC=
| AB2-BC2 |
| 252-202 |
则△ABC的面积为：
| 1 |
| 2 |
| 1 |
| 2 |
故答案为：150．
点评：本题考查了勾股定理以及三角函数，正确求得AC的长度是关键．
练习册系列答案
相关题目
如图，已知∠AOC=∠BOD=110°，∠BOC=75°，求：∠AOD的度数．
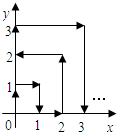如图，一个质点在第一象限及x轴、y轴上运动，在第一秒钟，它从原点（0，0）运动到（0，1），然后接着按图中箭头所示方向运动，即（0，0）→（0，1）→（1，1）→（1，0）→…，且每秒移动一个单位，那么第80秒时质点所在位置的坐标是（ ）| A、（0，9） |
| B、（9，0） |
| C、（0，8） |
| D、（ 8，0） |
观察下列图形：
请用你发现的规律直接求出图④中的数y和图⑤中的数x，则x+y=（ ）
请用你发现的规律直接求出图④中的数y和图⑤中的数x，则x+y=（ ）
| A、10 | B、-14 | C、-12 | D、6 |
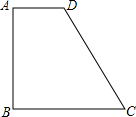如图，在直角梯形ABCD中，AD∥BC，AB⊥BC，AD=2，AB=3，BC=4，则CD的长是边长是6，8，10的三角形中最大边上的高的长是（ ）
| A、4.8 | B、2.4 |
| C、3.6 | D、7.5 |