题目内容
18.将一箱苹果分给若干位小朋友,若每位小朋友分5个苹果,则还剩12个苹果,若每位小朋友分8个苹果,则有一位小朋友分到了苹果但不足8个,则有小朋友5或6个,苹果37或42个.分析 设小朋友为x人,根据每位小朋友分5个苹果,则还剩12个苹果,表示出苹果的个数,再由每位小朋友分8个苹果,根据人数为x人,表示出需要苹果的个数,减去苹果的总数,即为最后一名小朋友分到的苹果数,再利用最后一位小朋友分到了苹果,但不足8个列出关于x的不等式,求出不等式的解集,在解集中找出正整数解得到x的值,即为小朋友的人数,即可得到一箱苹果的个数.
解答 解:设有x位小朋友,则苹果为(5x+12)个,
依题意得:0<8x-(5x+12)<8,
可化为:$\left\{\begin{array}{l}{3x-12>0}\\{3x-12<8}\end{array}\right.$,
解得:4<x<$\frac{20}{3}$,
∵x是正整数,
∴x取5或6,
当x=5时,5x+12=37;当x=6时,5x+12=42,
∴有两种情况满足题意:①这一箱苹果有37个,小朋友有5位;②这一箱苹果有42个,小朋友有6位,
故答案为:5或6;37或42.
点评 此题考查了一元一次不等式组的应用,其中根据题意表示出最后一名小朋友分到的苹果数是解本题的关键.

练习册系列答案
相关题目
9.在-2,3,0,1中,绝对值最小的数是( )
| A. | -2 | B. | -3 | C. | 0 | D. | 1 |
6.下列计算正确的是( )
| A. | (a2)3=a5 | B. | a2÷a2=0 | C. | (2a)2=2a2 | D. | a•a2=a3 |
3.已知∠A为锐角,且cosA=0.6,那么( )
| A. | 0°<∠A<30° | B. | 30°<∠A<45° | C. | 45°<∠A<60° | D. | 60°<∠A<90° |
7.下列计算正确的是( )
| A. | (-x3)2=-x6 | B. | x6-x4=x2 | C. | x9÷x3=x3 | D. | x2•x3=x5 |
8.反比例函数y=-$\frac{1}{x}$的图象在( )
| A. | 第一、三象限 | B. | 第一、二象限 | C. | 第二、四象限 | D. | 第三、四象限 |
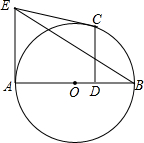 AB是的圆直径,从圆上一点C作CD⊥AB于D,圆在A,C两点的切线相交于E,证明:BE平分CD.
AB是的圆直径,从圆上一点C作CD⊥AB于D,圆在A,C两点的切线相交于E,证明:BE平分CD.