题目内容
3.已知∠A为锐角,且cosA=0.6,那么( )| A. | 0°<∠A<30° | B. | 30°<∠A<45° | C. | 45°<∠A<60° | D. | 60°<∠A<90° |
分析 先求出cos30°,cos45°及cos60°的近似值,再由余弦函数值随角增大而减小即可得出结论.
解答 解:∵cos30°=$\frac{\sqrt{3}}{2}$≈0.9,cos45°=$\frac{\sqrt{2}}{2}$≈0.7,cos60°=$\frac{1}{2}$=0.5,
∴45°<∠A<60°.
故选C.
点评 本题考查的是锐角三角函数的定义,熟知锐角三角函数的余弦函数值随角增大而减小是解答此题的关键.

练习册系列答案
相关题目
15.下列计算正确的是( )
| A. | a2•a5=a10 | B. | a3+a3=a6 | C. | (a3)2=a6 | D. | (2a)3=6a3 |
12.若反比例函数y=$\frac{2k+1}{x}$的图象位于第一、三象限,则k的取值可以是( )
| A. | -3 | B. | -2 | C. | -1 | D. | 0 |
13.下列计算正确的是( )
| A. | $2\sqrt{3}+5\sqrt{2}=7\sqrt{5}$ | B. | ${(\sqrt{3}+\sqrt{2})^2}=5$ | C. | $\sqrt{2a}+\sqrt{a}=\sqrt{3a}$ | D. | ${(\sqrt{3}-\sqrt{2})^2}=5-2\sqrt{6}$ |
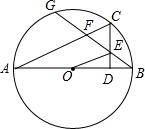 如图,AB是⊙O的直径,C是$\widehat{BG}$的中点,CD⊥AB于D,BG交CD、AC与E、F.求证:
如图,AB是⊙O的直径,C是$\widehat{BG}$的中点,CD⊥AB于D,BG交CD、AC与E、F.求证: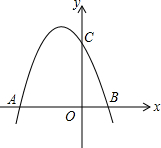 如图抛物线y=-x2+bx+c交x轴于点A(-3,0)和点B,交y轴于点C(0,3),
如图抛物线y=-x2+bx+c交x轴于点A(-3,0)和点B,交y轴于点C(0,3),