题目内容
如图,△ABC的边长分别为
、
、1,正六边形网格是由24个边长为1的正三角形组成,每个正三角形的顶点称为网格的格点.在下面三个正六边形网格中各画出一个三角形(画出三角形,并用阴影填充),使其同时满足下面三个条件:
(1)三个三角形的顶点都在格点上;
(2)三个三角形都与△ABC相似;
(3)三个三角形的面积大小都不同.并直接写出三个三角形与△ABC的相似比.
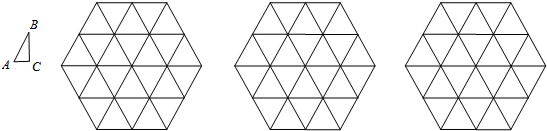
①相似比: ; ②相似比: ; ③相似比: .
| 1 |
| 2 |
| ||
| 2 |
(1)三个三角形的顶点都在格点上;
(2)三个三角形都与△ABC相似;
(3)三个三角形的面积大小都不同.并直接写出三个三角形与△ABC的相似比.

①相似比:
考点:作图—相似变换
专题:
分析:利用原三角形各边长,进而结合相似三角形的判定与性质分别求出即可.
解答:解:如图所示:
 .
.
 .
.点评:此题主要考查了相似三角形的判定与性质,结合各边长得出符合题意的图形是解题关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”,[a,b,c]称为“抛物线三角形系数”,若抛物线三角形系数为[-1,b,0]的“抛物线三角形”是等腰直角三角形,则b的值( )
| A、±2 | B、±3 | C、2 | D、3 |
 已知一次函数y=kx+b的图象如图,则关于x的不等式k(x-4)-2b>0的解集为( )
已知一次函数y=kx+b的图象如图,则关于x的不等式k(x-4)-2b>0的解集为( )| A、x>-2 | B、x<-2 |
| C、x>2 | D、x<3 |
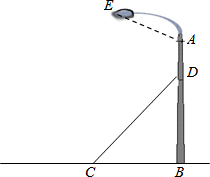 如图,某广场一灯柱AB被一钢缆CD固定,CD与地面成37°夹角,且CB=4米.
如图,某广场一灯柱AB被一钢缆CD固定,CD与地面成37°夹角,且CB=4米.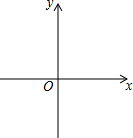 如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P.在新图形中你发现了什么?请写出一条;在若点P的坐标为(2a,b+1),则a与b的数量关系为
如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P.在新图形中你发现了什么?请写出一条;在若点P的坐标为(2a,b+1),则a与b的数量关系为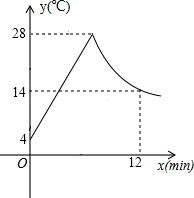 如图所示,制作某种食品的同时需将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟.据了解,该材料在加热过程中温度y与时间x成一次函数关系.已知该材料在加热前的温度为4℃,加热一段时间使材料温度达到28℃时停止加热,停止加热后,材料温度逐渐下降,这时温度y与时间x成反比例函数关系,已知当第12分钟时,材料温度是14℃.
如图所示,制作某种食品的同时需将原材料加热,设该材料温度为y℃,从加热开始计算的时间为x分钟.据了解,该材料在加热过程中温度y与时间x成一次函数关系.已知该材料在加热前的温度为4℃,加热一段时间使材料温度达到28℃时停止加热,停止加热后,材料温度逐渐下降,这时温度y与时间x成反比例函数关系,已知当第12分钟时,材料温度是14℃.