题目内容
15．
如图，已知四边形ABCD，其中A（1，1），B（2，2），C（0，3），D（-3，0），作出四边形ABCD关于原点对称的四边形A′B′C′D′．（1）写出点A′、B′、C′、D′的坐标；
（2）求四边形A′B′C′D′的面积．
分析 （1）首先作出A、B、C、D关于原点对称的点，然后顺次连接即可作出四边形ABCD关于原点对称的四边形A′B′C′D′，最后根据（x，y）关于原点的对称点的坐标是（-x，-y）即可求得点A′、B′、C′、D′的坐标；
（2）根据四边形A′B′C′D′为梯形，运用梯形面积公式进行计算，求得面积即可．
解答 解：（1）四边形ABCD关于原点对称的四边形A′B′C′D′如图所示，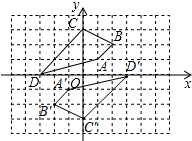
由题可得：A'（-1，-1），B'（-2，-2），C'（0，-3），D'（3，0）；
（2）四边形A′B′C′D′的面积=$\frac{（\sqrt{2}+3\sqrt{2}）×\frac{3}{2}\sqrt{2}}{2}$=6．
点评 本题主要考查了中心对称的作图以及中心对称的两个点坐标之间的关系，理解（x，y）关于原点的对称点的坐标是（-x，-y）是关键．
练习册系列答案
王后雄学案教材完全解读系列答案
相关题目