题目内容
17. 如图,过⊙O上一点E作圆的切线,交直径AC的延长线于点B,再取⊙O上一点D,连接AE、ED和CD,若⊙O的半径为2,∠EDC=30°,则CB的长为( )
如图,过⊙O上一点E作圆的切线,交直径AC的延长线于点B,再取⊙O上一点D,连接AE、ED和CD,若⊙O的半径为2,∠EDC=30°,则CB的长为( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 首先证明∠EOB=60°,在RT△BOE中,由OB=2OE,求出OB即可解决问题.
解答 解:如图, 连接OE,
连接OE,
∵∠A=∠EDC,∠EDC=30°,
∴∠A=30°,
∵OA=OE,
∴∠A=∠AEO=30°,
∴∠EOB=∠A+∠AEO=60°,
∵BE是切线,
∴∠BEO=90°,
∴∠B=30°,
在RT△BOE中,∵∠OEB=90°,OE=2,∠B=30°,
∴OB=2OE=4,
∵OC=2,
∴BC=OB-OC=4-2=2.
故答案为D.
点评 本题考查切线的性质、直角三角形中30度角所对的直角边等于斜边的一半等知识,解题的关键是灵活运用这些知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
8.( )的计算结果是1-x2.
| A. | (x-1)(x+1) | B. | (1+x)(1-x) | C. | (1-x)2 | D. | (1+x)2 |
2.平行四边形一边的长是10cm,那么这个平行四边形的两条对角线长可以是( )
| A. | 4 cm,6 cm | B. | 6 cm,8 cm | C. | 8 cm,12 cm | D. | 20 cm,30 cm |

 如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、B(0,1)、C(d,2).
如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、B(0,1)、C(d,2).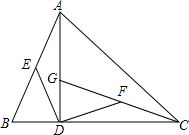 已知:如图,在△ABC中,∠ACB=45°,AD是边BC上的高,G是AD上一点,联结CG,点E、F分别是AB、CG的中点,且DE=DF.求证:△ABD≌△CGD.
已知:如图,在△ABC中,∠ACB=45°,AD是边BC上的高,G是AD上一点,联结CG,点E、F分别是AB、CG的中点,且DE=DF.求证:△ABD≌△CGD.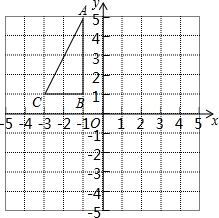 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-1,5),B(-1,1),C(-3,1).
如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-1,5),B(-1,1),C(-3,1).