题目内容
12.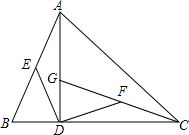 已知:如图,在△ABC中,∠ACB=45°,AD是边BC上的高,G是AD上一点,联结CG,点E、F分别是AB、CG的中点,且DE=DF.求证:△ABD≌△CGD.
已知:如图,在△ABC中,∠ACB=45°,AD是边BC上的高,G是AD上一点,联结CG,点E、F分别是AB、CG的中点,且DE=DF.求证:△ABD≌△CGD.
分析 先根据直角三角形的性质,得到AB=GC,再根据等腰直角三角形的性质,得到AD=CD,最后判定Rt△ABD≌Rt△CGD即可.
解答  证明:∵AD是边BC上的高,点E、F分别是AB、CG的中点,
证明:∵AD是边BC上的高,点E、F分别是AB、CG的中点,
∴DE=$\frac{1}{2}$AB,DF=$\frac{1}{2}$GC,
∵DE=DF,
∴AB=GC,
∵∠ACB=45°,AD是边BC上的高,
∴∠CAD=45°,
∴∠CAD=∠ACD,
∴AD=CD,
在Rt△ABD和Rt△CGD中,
$\left\{\begin{array}{l}{AD=CD}\\{AB=CG}\end{array}\right.$,
∴Rt△ABD≌Rt△CGD(HL).
点评 本题主要考查了全等三角形的判定方法,证明时注意:在直角三角形中,斜边上的中线等于斜边的一半,即直角三角形的外心位于斜边的中点.

练习册系列答案
相关题目
20.在2,0,-3,-5中,最小的数是( )
| A. | 2 | B. | -5 | C. | -3 | D. | 0 |
7.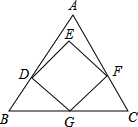 一个正方形和一个等边三角形的位置如图所示摆放,点G是BC中点,正方形对角线EG⊥BC,则∠AFE=( )
一个正方形和一个等边三角形的位置如图所示摆放,点G是BC中点,正方形对角线EG⊥BC,则∠AFE=( )
 一个正方形和一个等边三角形的位置如图所示摆放,点G是BC中点,正方形对角线EG⊥BC,则∠AFE=( )
一个正方形和一个等边三角形的位置如图所示摆放,点G是BC中点,正方形对角线EG⊥BC,则∠AFE=( )| A. | 10° | B. | 15° | C. | 20° | D. | 25° |
17. 如图,过⊙O上一点E作圆的切线,交直径AC的延长线于点B,再取⊙O上一点D,连接AE、ED和CD,若⊙O的半径为2,∠EDC=30°,则CB的长为( )
如图,过⊙O上一点E作圆的切线,交直径AC的延长线于点B,再取⊙O上一点D,连接AE、ED和CD,若⊙O的半径为2,∠EDC=30°,则CB的长为( )
 如图,过⊙O上一点E作圆的切线,交直径AC的延长线于点B,再取⊙O上一点D,连接AE、ED和CD,若⊙O的半径为2,∠EDC=30°,则CB的长为( )
如图,过⊙O上一点E作圆的切线,交直径AC的延长线于点B,再取⊙O上一点D,连接AE、ED和CD,若⊙O的半径为2,∠EDC=30°,则CB的长为( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
4.若分式$\frac{2x+y}{xy}$中,x、y的值都扩大3倍,则原分式的值( )
| A. | 扩大3倍 | B. | 缩小3倍 | C. | 不变 | D. | 无法确定 |
2.下列方程中,是一元二次方程的是( )
| A. | x2+2x-4=0 | B. | 6x2+2=6x2-x | C. | -3x+2=0 | D. | x2+2xy-3y2=0 |
