题目内容
8.(1)计算:(-3)2+|-2|-20150-$\sqrt{9}$+($\frac{1}{2}$)-2(2)解不等式组:$\left\{\begin{array}{l}{4x-3<3(2x+1)}\\{\frac{3}{2}x-1≤5-\frac{1}{2}x}\end{array}\right.$并在数轴上把解集表示出来.
分析 (1)原式第一项利用乘方的意义计算,第二项利用绝对值的代数意义化简,第三项利用零指数幂法则计算,第四项利用算术平方根定义计算,最后一项利用负整数指数幂法则计算即可得到结果;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分确定出解集,表示在数轴上即可.
解答 解:(1)原式=9+2-1-3+4=11;
(2)$\left\{\begin{array}{l}{4x-3<3(2x+1)①}\\{\frac{3}{2}x-1≤5-\frac{1}{2}x②}\end{array}\right.$,
由①得:x>-3,
由②得:x≤3,
∴不等式组的解集为-3<x≤3,
点评 此题考查了实数的运算,解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16. 如图,一圆弧形钢梁的拱高CD为8m,跨径AB为40m,则这钢梁圆弧的半径是( )
如图,一圆弧形钢梁的拱高CD为8m,跨径AB为40m,则这钢梁圆弧的半径是( )
 如图,一圆弧形钢梁的拱高CD为8m,跨径AB为40m,则这钢梁圆弧的半径是( )
如图,一圆弧形钢梁的拱高CD为8m,跨径AB为40m,则这钢梁圆弧的半径是( )| A. | 28m | B. | 29m | C. | 30m | D. | 31m |
13.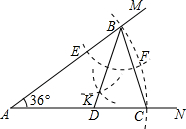 如图,小明作图如下:
如图,小明作图如下:
(1)用量角器作∠MAN=36°;
(2)以A为圆心适当长为半径作圆弧,分别交AM,AN于B,C两点,连结BC;
(3)以B为圆心适当长为半径作圆弧,分别交AB,BC于E,F两点,再分别以E,F为圆心大于$\frac{1}{2}$EF长为半径作圆弧,两条圆弧交于点K,连结BK并延长交AC于点D.
若AD=a,则由以上作图可得AB为( )
 如图,小明作图如下:
如图,小明作图如下:(1)用量角器作∠MAN=36°;
(2)以A为圆心适当长为半径作圆弧,分别交AM,AN于B,C两点,连结BC;
(3)以B为圆心适当长为半径作圆弧,分别交AB,BC于E,F两点,再分别以E,F为圆心大于$\frac{1}{2}$EF长为半径作圆弧,两条圆弧交于点K,连结BK并延长交AC于点D.
若AD=a,则由以上作图可得AB为( )
| A. | $\frac{\sqrt{5}-1}{2}$a | B. | $\frac{3-\sqrt{5}}{2}$a | C. | $\frac{\sqrt{5}+1}{2}a$ | D. | $\frac{3+\sqrt{5}}{2}$a |
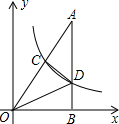 如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=$\frac{k}{x}$(x>0)经过斜边OA的中点C,与另一直角边交于点D,若S△OCD=3,则k的值为4.
如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=$\frac{k}{x}$(x>0)经过斜边OA的中点C,与另一直角边交于点D,若S△OCD=3,则k的值为4.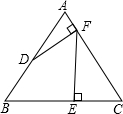 如图,已知:等边三角形ABC,点D是AB的中点,过点D作DF⊥AC,垂足为F,过点F作FE⊥BC,垂足为E,若三角形ABC的边长为4.则线段BE的长为$\frac{5}{2}$.
如图,已知:等边三角形ABC,点D是AB的中点,过点D作DF⊥AC,垂足为F,过点F作FE⊥BC,垂足为E,若三角形ABC的边长为4.则线段BE的长为$\frac{5}{2}$.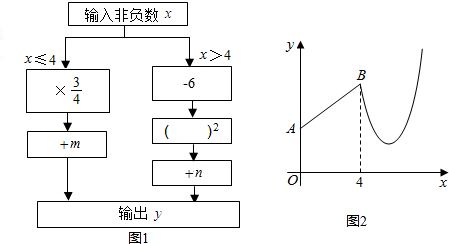
 某商场为促进消费,方便消费者停车,拟将商场门口某区域改建为停车场.如图,已知该区域边界处有台阶五级,每个台阶高150mm,宽300mm,现把台阶处改建为斜坡以方便汽车出入,为保证不损坏车的底盘,台阶下面设置缓坡带,使斜坡的倾斜角为5.711°,则台阶下面增加缓坡带的水平宽OA为多少m?(参考数据tan5.711°≈0.1000,sin5.711°≈0.09951,cos5.711°≈0.9950).
某商场为促进消费,方便消费者停车,拟将商场门口某区域改建为停车场.如图,已知该区域边界处有台阶五级,每个台阶高150mm,宽300mm,现把台阶处改建为斜坡以方便汽车出入,为保证不损坏车的底盘,台阶下面设置缓坡带,使斜坡的倾斜角为5.711°,则台阶下面增加缓坡带的水平宽OA为多少m?(参考数据tan5.711°≈0.1000,sin5.711°≈0.09951,cos5.711°≈0.9950).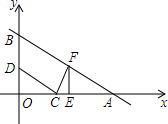 如图,在平面直角坐标系中,一次函数图象与x轴,y轴分别交于点A(8,0),B(0,4),点C的坐标为(3,0),动点D是射线BO上一个动点,连结CD,过点C作CD⊥FC,交一次函数图象于点F.
如图,在平面直角坐标系中,一次函数图象与x轴,y轴分别交于点A(8,0),B(0,4),点C的坐标为(3,0),动点D是射线BO上一个动点,连结CD,过点C作CD⊥FC,交一次函数图象于点F.