题目内容
3.图1是一种数值转换器的示意图,图2是小敏按照其对应关系画出的y关于x的函数图象.已知点A的坐标为(0,3),点B的横坐标为4.(1)求m,n的值和输出y的最小值;
(2)当y=5时,求x的值.
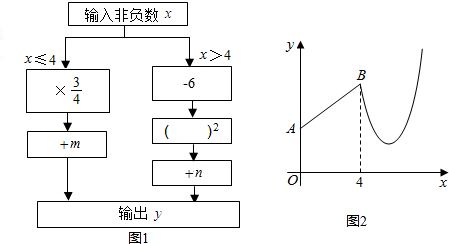
分析 (1)根据数值转换器,可得函数解析式,根据待定系数法,可得函数解析式;根据顶点坐标是函数的最值,可得答案;
(2)根据自变量与函数值的对应关系,可得相应自变量的值.
解答 解:(1)由数值转换器,得
y=$\left\{\begin{array}{l}{\frac{3}{4}x+m(0≤x≤4)}\\{(x-6)^{2}+n(x>4)}\end{array}\right.$,
当x=0时,y=m=3,
当x=4时,y=3+3=6,即B(4,6).
将B点坐标代入y=(x-6)2+n,得
4+n=6,解得n=2;
当x=6时,y最小=n=2;
(2)当y=5时,$\frac{3}{4}$x+3=5,解得x=$\frac{8}{3}$,
当y=5时,(x-6)2+2=5,解得x1=6+$\sqrt{3}$,x2=6-$\sqrt{3}$.
点评 本题考查了二次函数图象,利用待定系数法求函数解析式是解题关键,又利用了二次函数的性质得出自变量与函数值的对应关系.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目

 如图,△ABC的顶点在正方形网格的格点处,则tanB的值为1.
如图,△ABC的顶点在正方形网格的格点处,则tanB的值为1. 如图,抛物线y=ax2+bx+c的对称轴为直线x=-1,且经过点(1,0),则9a-3b+c的值是( )
如图,抛物线y=ax2+bx+c的对称轴为直线x=-1,且经过点(1,0),则9a-3b+c的值是( )