题目内容
19.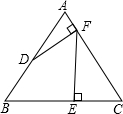 如图,已知:等边三角形ABC,点D是AB的中点,过点D作DF⊥AC,垂足为F,过点F作FE⊥BC,垂足为E,若三角形ABC的边长为4.则线段BE的长为$\frac{5}{2}$.
如图,已知:等边三角形ABC,点D是AB的中点,过点D作DF⊥AC,垂足为F,过点F作FE⊥BC,垂足为E,若三角形ABC的边长为4.则线段BE的长为$\frac{5}{2}$.
分析 根据在直角三角形中,30°角所对的直角边等于斜边的一半,求得AF,CF,CE,再由三角形ABC的边长为4,得出BE的长.
解答 解:∵△ABC为等边三角形,
∴∠A=∠C=60°AB=AC=4,
∵DF⊥AC,FE⊥BC,
∴∠AFD=∠CEF=90°,
∴∠ADF=∠CFE=30°,
∴AF=$\frac{1}{2}$AD,CE=$\frac{1}{2}$CF,
∵点D是AB的中点,
∴AD=2,
∴AF=1,CF=3,CE=$\frac{3}{2}$,
∴BE=$\frac{5}{2}$.
故答案为$\frac{5}{2}$.
点评 本题考查了等边三角形的性质,以及含30°角直角三角形的性质,30°角所对的直角边等于斜边的一半,掌握性质是解题的关键.

练习册系列答案
相关题目
7.为了鼓励市民节约用水,某市自来水公司对每户用水量进行了分段计费,每户每月用水量在规定吨数以下的收费标准相同,规定吨数以上的超过部分收费相同.如表是小明家1-4月用水量和交费情况:
(1)自来水公司规定用水量为8吨,规定用量的收费标准是2元/吨,超过部分收费3元/吨.
(2)若小明家5月份用水25吨,则应缴多少元水费?
(3)若小明6月份缴水费43元,则6月份他们家用水多少吨?
| 月份 | 1 | 2 | 3 | 4 |
| 用水量(吨) | 6 | 8 | 12 | 15 |
| 费用(元) | 12 | 16 | 28 | 37 |
(2)若小明家5月份用水25吨,则应缴多少元水费?
(3)若小明6月份缴水费43元,则6月份他们家用水多少吨?
9.下列说法正确的是( )
| A. | 所有的有理数都能用数轴上的点表示 | |
| B. | 符号不同的两个数互为相反数 | |
| C. | 有理数分为正数和负数 | |
| D. | 两数相加,和一定大于任何一个数 |
 如图,△ABC的顶点在正方形网格的格点处,则tanB的值为1.
如图,△ABC的顶点在正方形网格的格点处,则tanB的值为1. 如图,在△AOC和△BOC中,若∠AOC=∠BOC,添加一个条件AO=BO,使得△AOC≌△BOC.
如图,在△AOC和△BOC中,若∠AOC=∠BOC,添加一个条件AO=BO,使得△AOC≌△BOC.